1 2 1 6 1 19 Newtons Law

第一章 作业 1. 2 1. 6 1. 19 Newton’s Law of Viscosity(牛顿内摩擦定律) ： is dynamic viscosity， N s/m 2 (Pa s) Kinematic viscosity (运动粘度) (m 2/s) specific weight (重度) , specific gravity (比重) S , modulus of elasticity(体积弹性模量) K

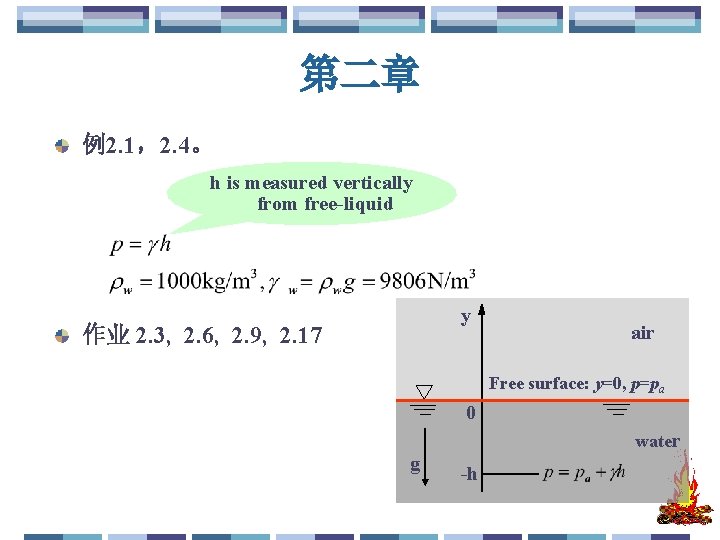
第二章 例2. 1，2. 4。 h is measured vertically from free-liquid y 作业 2. 3, 2. 6, 2. 9, 2. 17 air Free surface: y=0, p=pa 0 water g -h

2. 6 Bourdon gage A inside a pressure tank reads 12 psi. Another bourdon gage B outside the pressure tank and connected with it reads 20 psi, and an aneroid barometer( 无液气压表) reads 30 in Hg. What is the absolute pressure measured by A in inches of mercury? Solution:

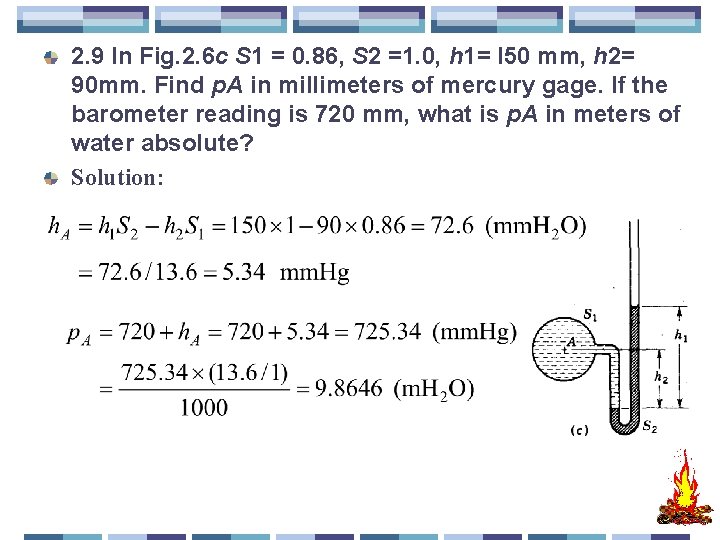
2. 9 In Fig. 2. 6 c S 1 = 0. 86, S 2 =1. 0, h 1= l 50 mm, h 2= 90 mm. Find p. A in millimeters of mercury gage. If the barometer reading is 720 mm, what is p. A in meters of water absolute? Solution:

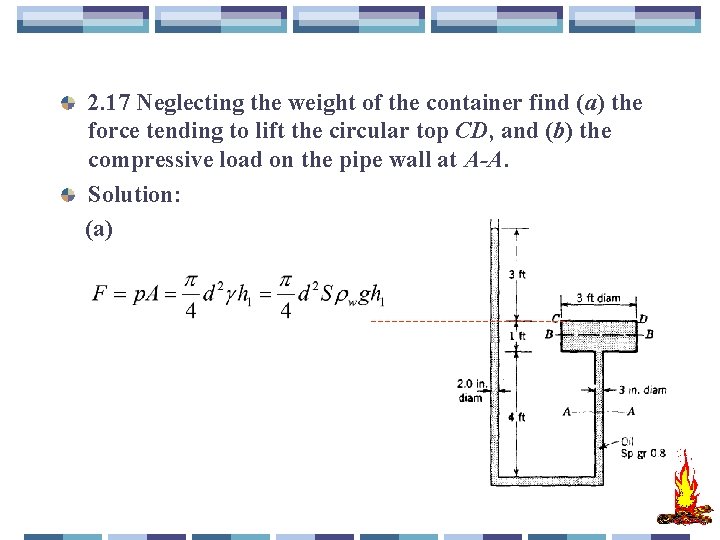
2. 17 Neglecting the weight of the container find (a) the force tending to lift the circular top CD, and (b) the compressive load on the pipe wall at A-A. Solution: (a)

第三章 例3. 14, 3. 16, 3. 19 作业 3. 9, 3. 16, 3. 19 path of a particle(迹线) ，Streamline (流线)，stream tube( 流管) continuity equation (连续性方程), (for incompressible, steady flow) 断面平均速度 Bernoulli equation（伯努利方程）

3. 9 Neglecting losses, determine the discharge in Fig. 3. 35. Solution:

3. 16 The 图 3. 38中显示的水泵系统中，当泵的入口处开始气穴时，压强为 3. 16 pumping system shown in Fig. 3. 38 must have pressure of 34. 47 k. Pa in the discharge line when cavitation is incipient(开始的) at the pump inlet. 34. 47 k. Pa。计算这种运行条件下从水库到泵的管道长度，管道的损失表 Calculate the length of pipe from the reservoir to the pump for this operating 2/2 g)(0. 03 L/D)。泵供给流体的马力（功率）是多少？百分之多少 示为(V 1 condition if the loss in this pipe can be expressed as (V 12/2 g)(0. 03 L/D). What 的功率用来克服流动损失？气压计（测出的是当地大气压）的读数是 762 horsepower is being supplied to the fluid by the pump? What percent of this mm Hg。 power is being used to overcome losses? Barometer reads 762 mm Hg. Solution: By neglecting the loss between the gage and the outlet, (忽略泵 出口和管道出口之间的损失，以管道出口为 0截面，泵出口（表压计所在截面） 为g截面，在此两截面应用能量方程。) By application of continuity equation(连续性方程) V 1 V 0

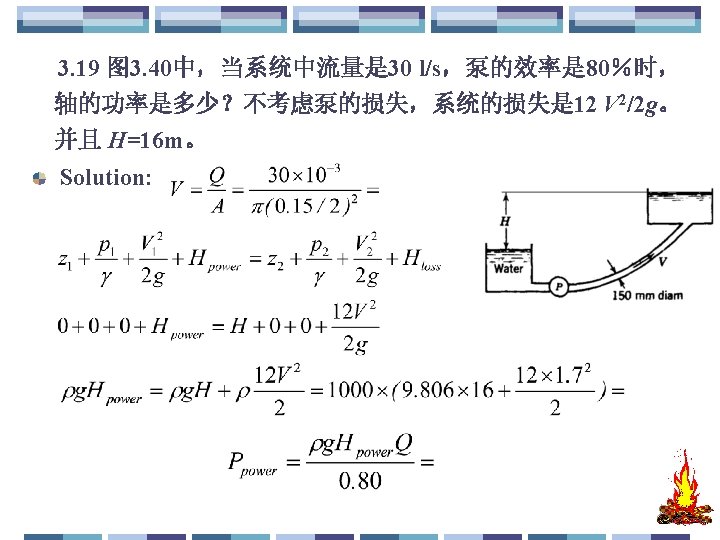
3. 19 图 3. 40中，当系统中流量是 30 Determine the shaft horsepower for an 80 percent 3. 19 l/s，泵的效率是 80％时， efficient pump to discharge 30 l/s through the system of 2 轴的功率是多少？不考虑泵的损失，系统的损失是 12 V /2 g。 Fig. 3. 40. The system losses, exclusive of pump losses, are 12 并且 H=16 m。 V 2/2 g, and H=16 m. Solution:

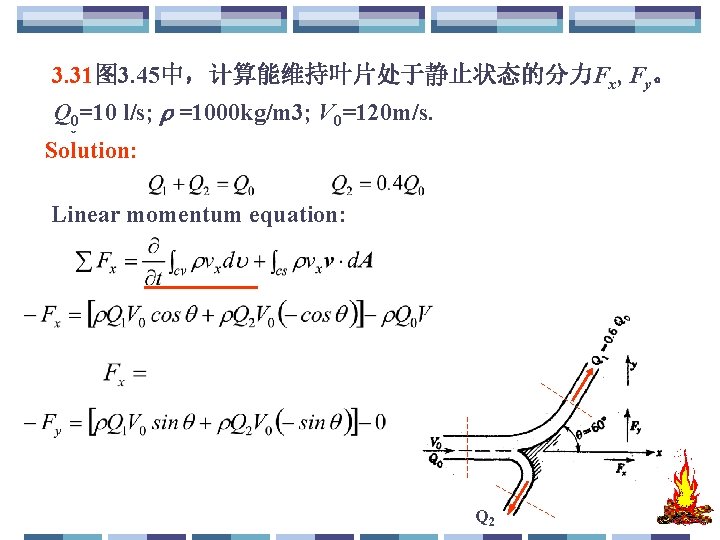
3. 31 Calculate the force components Fx, Fy needed to hold the 3. 31图 3. 45中，计算能维持叶片处于静止状态的分力Fx, Fy。 stationary vane of Fig. 3. 45. Q 0=10 l/s; =1000 kg/m 3; Q =10 l/s; =1000 kg/m 3; V 0=120 m/s. V 00=120 m/s. Solution: Linear momentum equation: Q 2

第四章 例4. 8； 作业 4. 1, 4. 2, 4. 13，4. 20, 4. 26 Reynolds number(雷诺数) round tubes (圆管) Laminar flow(层流): Re<2000； Turbulent flow(紊流): Re>2000

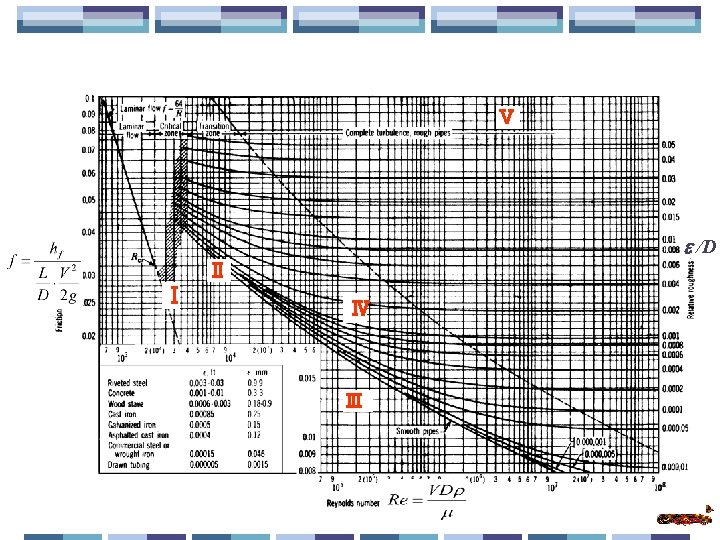
Energy equation (能量方程) laminar flow: =2； turbulent flow: =1 沿程损失 f is friction factor(沿程阻力系数)。 Minor losses(局部损失) （出口数，入口数；按出口速 度系数计算） Laminar flow, Re<2000

Solution 2: U=0. 7 m/s， a=0. 05× 10 3 m， =1 P =0. 1 Pa s

4. 9对一个内径为 3 mm的水平管，在Re Determine the pressure drop per meter of 3 -mm-ID = 4. 9 = 200时，流体的μ horizontal tubing for flow of liquid, μ = 60 c. P, sp gr = 0. 83, 60 atc. P, Re 比重S= = 200. 0. 83, 求流体每米压降。 Solution:

4. 13 test on 300 -mm-diameter pipe with water showed a 4. 13 A在直径300 mm的 流体为水的管道上的实验显示，水银 gage difference of 280 mm on a mercury-water manometer －水差压计在相距L=120 m的两端的压强差为 280 mm Hg， connected to two piezometer rings l 20 m apart, The flow was 流量是 0. 23 m 3/s，摩擦系数f 0. 23 m 3/s. What is the friction是多少？ factor? Solution:

2的水， 4. 20 A 60 -mm-diameter smooth pipe 150 m long. MN/m conveys 10 l/s 4. 20 温度 25℃，来自于水主管压强为p=1. 6 water at 25℃ from a water main p=1. 6 MN/m 2 l/s , to的光滑管流 the top of a 经直径为 60 mm，长为 150 m，水流量为 10 building 25 m above the main, What pressure can be 到主管道上25 m高的建筑物的顶部，在建筑物的顶部的压 maintained 强是多少? at the top of the building? Solution: p=1. 6 106 Pa, Q=10 10 3 m 3/s, l=150 m, d=60 10 3 m, HT=25 m, At 25 C, =997 kg/m 3, =0. 893 10 6 m 2/s ( =1000 kg/m 3(at 4 C), =1 10 10 6 m 2/s (at 20 C). ) smooth pipe(光滑管)：f只与雷诺数有关，与相对粗糙度ε/D 无关，在穆迪图上是一条直线。From the Moody diagram f=0. 015, The energy equation applied between the main and the top of the building, including the losses except of the minor losses.

第五章 作业 5. 4 Orifice in a pipe(管道上小孔流) Discharge coefficient(流量系数)Cd，A is area of orificce(小孔的面积) 1 D p 1 1 c 2 p 2 d c 2

5. 4 Compute the discharge from the tank shown in Fig. 5. 10. Solution: (page 103)