1 1 Understanding Points Lines and Planes All

1. 1 Understanding Points, Lines, and Planes All figures in Geometry are made of points, lines, and planes; however, these terms are undefined.

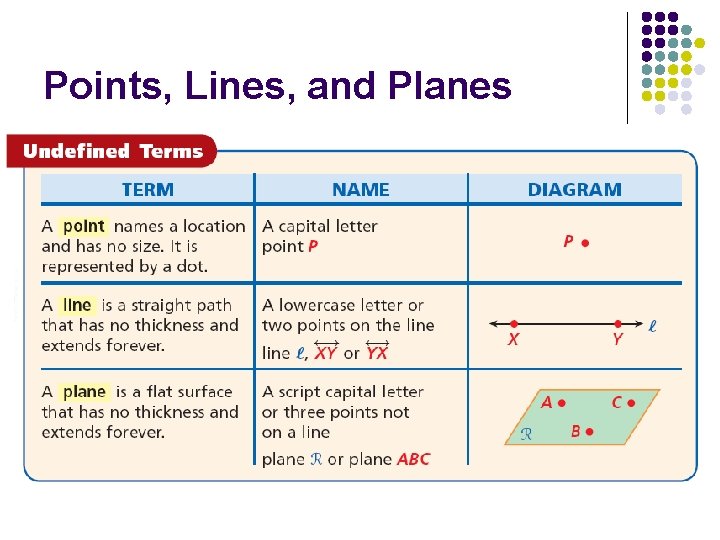
Undefined Terms The most basic figures in geometry are undefined terms, which cannot be defined by using other figures. The undefined terms point, line, and plane are the building blocks of geometry.

Points, Lines, and Planes

Colinear and Coplanar Points that lie on the same line are collinear. K, L, and M are collinear. K, L, and N are noncollinear. Points that lie on the same plane are coplanar. Otherwise they are noncoplanar. K L M N

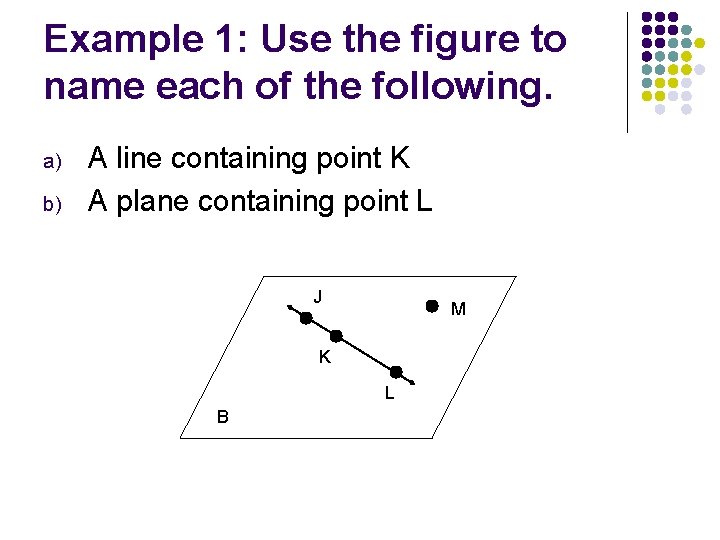
Example 1: Use the figure to name each of the following. a) b) A line containing point K A plane containing point L J M K L B

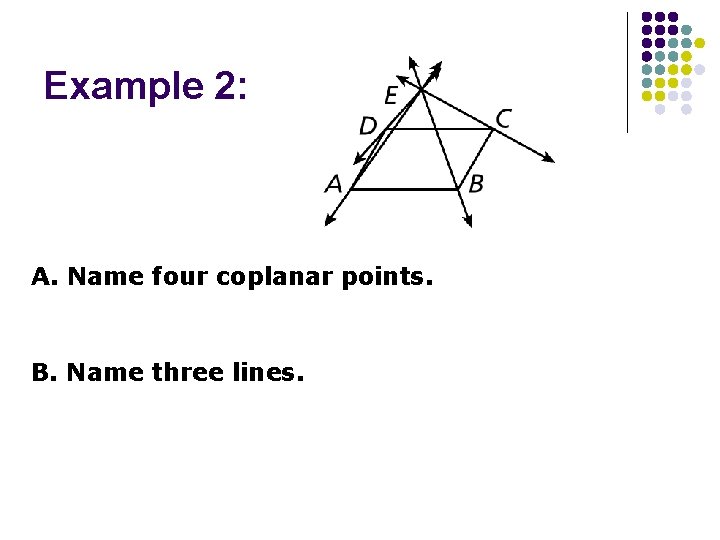
Example 2: A. Name four coplanar points. B. Name three lines.

Example 3: Draw and label a figure for each relationship. a) Plane R contains lines AB and DE, which intersect at point P. Add point C on plane R so that it is not collinear with AB or DE. b) QR on a coordinate plane contains Q(-2, 4) and R(4, -4). Add point T so that T is collinear with these points.

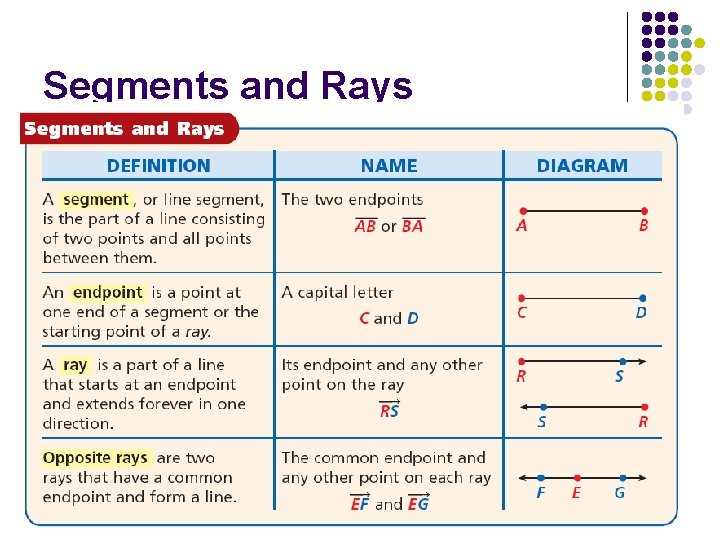
Segments and Rays

Example 4: Draw and label each of the following. A. a segment with endpoints M and N. B. opposite rays with a common endpoint T. C. Draw and label a ray with endpoint M that contains N.

Postulate A postulate, or axiom, is a statement that is accepted as true without proof. Postulates about points, lines, and planes help describe geometric properties.

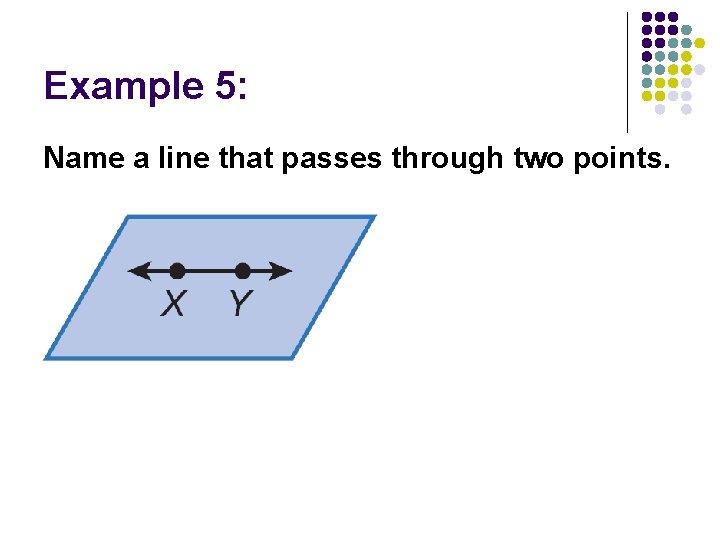
Example 5: Name a line that passes through two points.

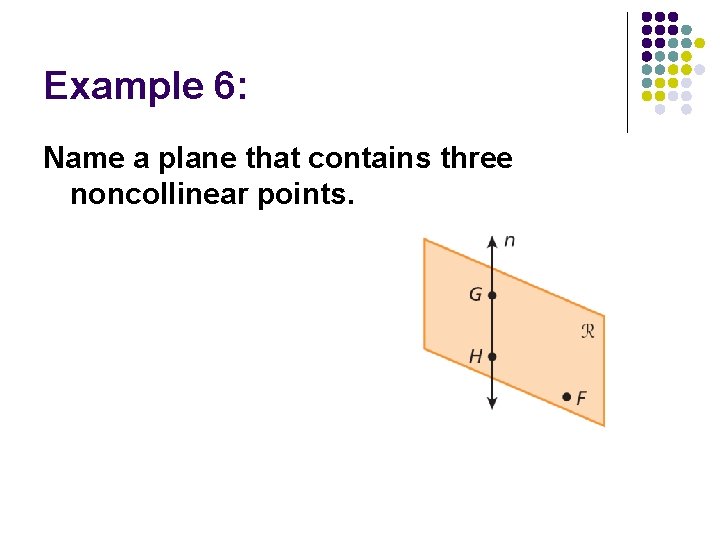
Example 6: Name a plane that contains three noncollinear points.

Modeling intersections l Recall that a system of equations is a set of two or more equations containing two or more of the same variables. The coordinates of the solution of the system satisfy all equations in the system. These coordinates also locate the point where all the graphs of the equations in the system intersect. l An intersection is the set of all points that two or more figures have in common. The next two postulates describe intersections involving lines and planes.

More Postulates

Example 7: A. Sketch two lines intersecting in exactly one point. B. Sketch a figure that shows a line that lies in a plane. C. Sketch a figure that shows two lines intersect in one point in a plane, but only one of the lines lies in the plane.

Creating and interpreting 3 D drawings is vital to such fields as architecture, engineering, and computer gaming.

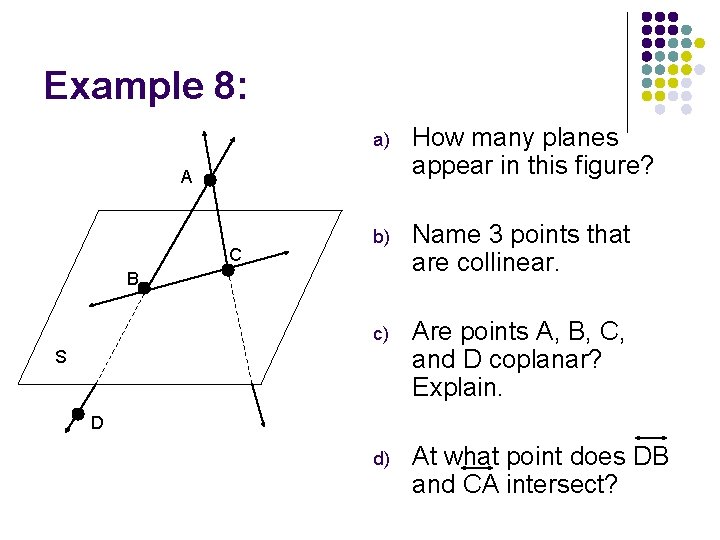
Example 8: a) How many planes appear in this figure? b) Name 3 points that are collinear. c) Are points A, B, C, and D coplanar? Explain. d) At what point does DB and CA intersect? A C B S D

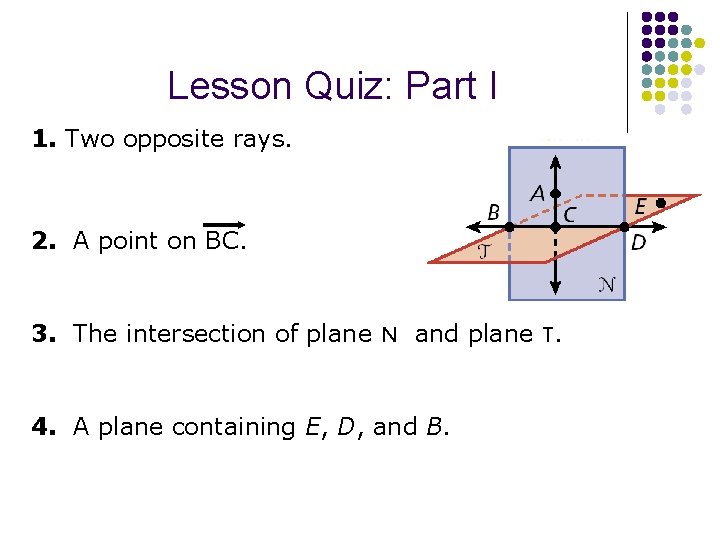
Lesson Quiz: Part I 1. Two opposite rays. 2. A point on BC. 3. The intersection of plane N and plane T. 4. A plane containing E, D, and B.

Lesson Quiz: Part II Draw each of the following. 5. a line intersecting a plane at one point 6. a ray with endpoint P that passes through Q