1 1 Some Basics of Algebra Algebraic Expressions

1. 1 Some Basics of Algebra • Algebraic Expressions and Their Use • Translating to Algebraic Expressions • Evaluating Algebraic Expressions • Sets of Numbers

Terminology A letter that can be any one of various numbers is called a variable. If a letter always represents a particular number that never changes, it is called a constant.

Algebraic Expressions An algebraic expression consists of variables, numbers, and operation signs. Examples: When an equal sign is placed between two expressions, an equation is formed.

Translating to Algebraic Expressions Key Words Addition add sum of plus Subtraction subtract difference of minus increased by decreased by more than less than Multiplication multiply product of times Division divided by quotient of twice ratio of per

Example Translate to an algebraic expression: Eight more than twice the product of 5 and a number. Solution Eight more than twice the product of 5 and a number.

Evaluating Algebraic Expressions When we replace a variable with a number, we are substituting for the variable. The calculation that follows is called evaluating the expression.

Example Evaluate the expression Solution 8 xz – y = 8· 2· 3 – 7 = 48 – 7 = 41 Substituting Multiplying Subtracting

Example The base of a triangle is 10 feet and the height is 3. 1 feet. Find the area of the triangle. Solution h 10· 3. 1 = 15. 5 square feet b

Exponential Notation The expression an, in which n is a counting number means n factors In an, a is called the base and n is called the exponent, or power. When no exponent appears, it is assumed to be 1. Thus a 1 = a.

Rules for Order of Operations 1. Simplify within any grouping symbols. 2. Simplify all exponential expressions. 3. Perform all multiplication and division working from left to right. 4. Perform all addition and subtraction working from left to right.

Example Evaluate the expression Solution 2(x + 3)2 – 12 x 2 = 2(2 + 3)2 – 12 22 Substituting Working within parentheses Simplifying 52 and 22 Multiplying and Dividing Subtracting

Example Evaluate the expression Solution 4 x 2 + 2 xy – z = 4· 32 + 2· 3· 2 – 8 = 4· 9 + 2· 3· 2 – 8 = 36 + 12 – 8 = 40 Substituting Simplifying 32 Multiplying Adding and Subtracting

Part 2 of 1. 1 Sets of Numbers

Sets of Numbers Natural Numbers (Counting Numbers) Numbers used for counting: {1, 2, 3, …} Whole Numbers The set of natural numbers with 0 included: {0, 1, 2, 3, …} Integers The set of all whole numbers and their opposites: {…, -3, -2, -1, 0, 1, 2, 3, …}

Sets of Numbers Rational Numbers that can be expressed as an integer divided by a nonzero integer are called rational numbers:

Converting Fractions to Decimals Divide the numerator by the denominator . 8 3 3 3 6 5. 0 0 0 7 48 8 20 9 18 10 20

Any fraction can be converted to a repeating decimal or a terminating decimal. .

All integers can be written as fractions. Insert a denominator of 1. Look at the following conclusion.

Rationals include the following. • All integers (-2, 5, 17, 0) • All fractions (proper, improper, or mixed) • All terminating decimals • All repeating decimals -2. 34, 0. 0456

Sets of Numbers like are said to be irrational. Decimal notation for irrational numbers neither terminates nor repeats. Real Numbers that are either rational or irrational are called real numbers:

Identify as natural, whole, integers, rational, or irrational. -3 0. 457 10 0 6. 2

Answers • Natural: 10 • Whole: 10 • Integers: 10 • Rational: • Irrational: 0 0 -3

Set Notation Roster notation: {2, 4, 6, 8} Set-builder notation: {x | x is an even number between 1 and 9} “The set of all x such that x is an even number between 1 and 9”

Write with Roster Notation

Write with Set-Builder Notation 1) 5) The set of all integers between -6 and 1

Elements and Subsets If B = { 1, 3, 5, 7}, we can write 3 B to indicate that 3 is an element or member of set B. We can also write 4 B to indicate that 4 is not an element of set B. When all the members of one set are members of a second set, the first is a subset of the second. If A = {1, 3} and B = { 1, 3, 5, 7}, we write A B to indicate that A is a subset of B.

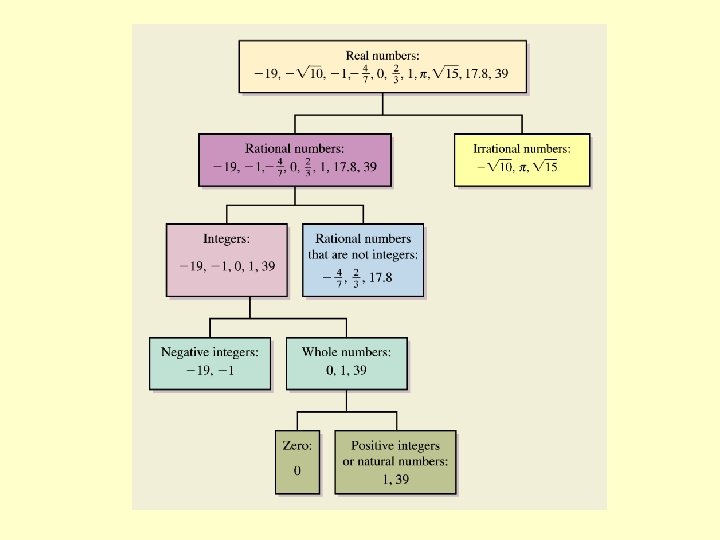
True or False? Use the following sets: N= Naturals, W = Wholes, Z = integers, Q = Rationals, H = Irrationals, and R = Reals

Answers • • • False True False