1 1 Real Numbers Relations Functions Learning Goals

Definition The Real Number System: Real Numbers Rational Numbers Irrational Numbers

Definition Rational Numbers can be expressed in the form where r and s are integers and. Rational numbers can be written as a decimal that either terminates or repeats in a pattern.

Example Rational Numbers: -3 5

Important Idea A rational number is a number that can be found on a number line. -4 0 1 5

Definition Irrational Numbers are numbers that cannot be expressed in the form and cannot be found on a number line.

Example Irrational Numbers:

Important Idea Any number that cannot be written as a decimal that either terminates or repeats in a pattern is an irrational number. Square roots of numbers that are not perfect squares are always irrational.

Important Idea Numbers such as are called irrational numbers and are always between two other numbers.

Important Idea. . . If is always between two numbers, where exactly is it? Could it be that it doesn’t exist ? ? ?

Try This True or False: is an irrational number. False

Try This On a sheet of paper, list the differences between a rational number and an irrational number.

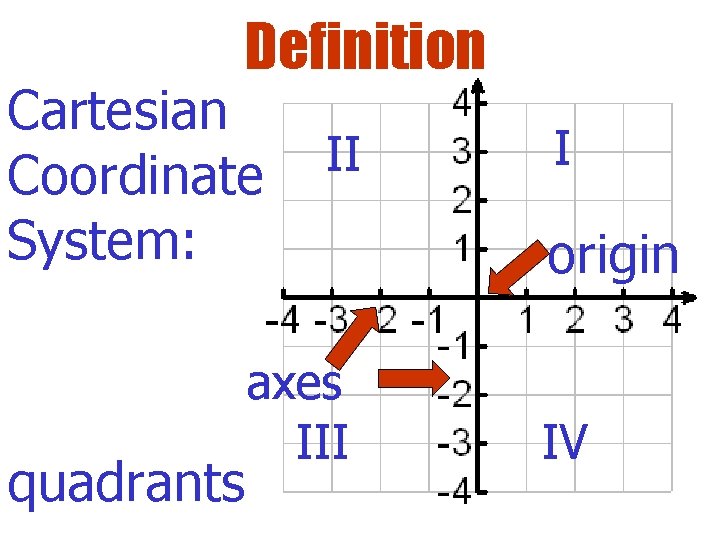
Definition Cartesian Coordinate System: quadrants II axes III I origin IV

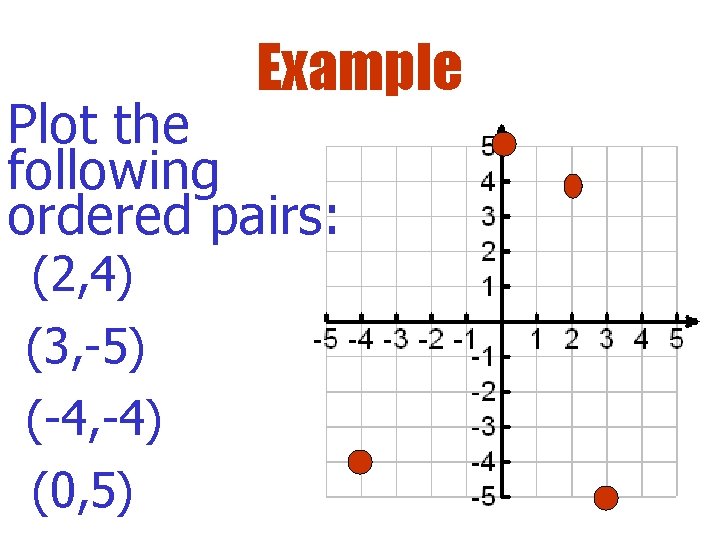
Example Plot the following ordered pairs: (2, 4) (3, -5) (-4, -4) (0, 5)

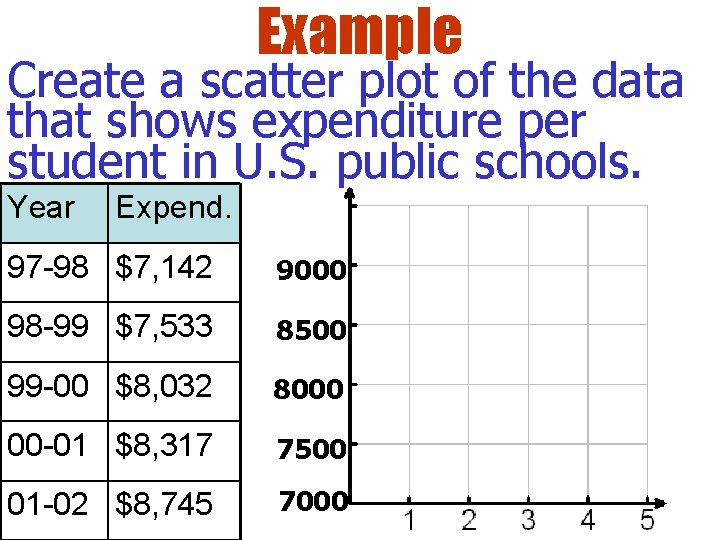
Example Create a scatter plot of the data that shows expenditure per student in U. S. public schools. Year Expend. 97 -98 $7, 142 9000 98 -99 $7, 533 8500 99 -00 $8, 032 8000 00 -01 $8, 317 7500 01 -02 $8, 745 7000

Definition The Domain is all the possible values that x can have. The Range is all the possible values that y can have. f(x) is another name for y.

Example The table shows the height and arm span in cm. of six members of the cheerleading squad: Height 178 189 158 169 195 188 Arm Span 180 163 169 182 Write the relation’s domain and range using set notation.

Example Given the relation {(0, 1), (1, 2), (-1, 2), (2, 5)(3, 10), (-3, 10)}, state its domain & range, create a scatter plot and find a rule that relates the value of the first coordinate to the value of the second coordinate.

Try This Given the relation {(0, 0), (1, 1), (1, -1), (4, 2)(9, 3), (9, -3)}, state its domain & range, create a scatter plot and find a rule that relates the value of the first coordinate to the value of the second coordinate.

Solution Domain={0, 1, 4, 9} Range={-3, -2, -1, 0, 1, 2, 3} Rule: or Lists: Scatter Plot:

Definition A function is a set of ordered pairs such that the first coordinate denotes the input, the second coordinate denotes the output that is obtained from the rule of the function, and each input corresponds to one and only one output.

Important Idea A function is like a meat grinder. You put something in (Domain), turn the crank (implement the Rule), and collect the output (Range).

Important Idea The idea of a function is one of the most important in all of mathematics. Business, computer programs, science, economics and medicine all depend on the idea of a function.

Example C=9. 95+ (1000*. 128) +(kwh 1000)*. 128

Example In the following sets of ordered pairs, the first coordinate represents an input and the second coordinate represents the corresponding output. Explain why each set is, or is not, a function. a) {(0, 1), (-1, 3), (2, 4), (2, -1)} b) {(0, 1), (-1, 3), (2, 4), (3, -1)}

Try This In the following set of ordered pairs, the first coordinate represents an input and the second coordinate represents the corresponding output. Explain why each set is, or is not, a function. a) {(0, 1), (1, 3), (2, 4), (3, 5)} b) {(0, 1), (2, 3), (2, 4), (3, 5)}

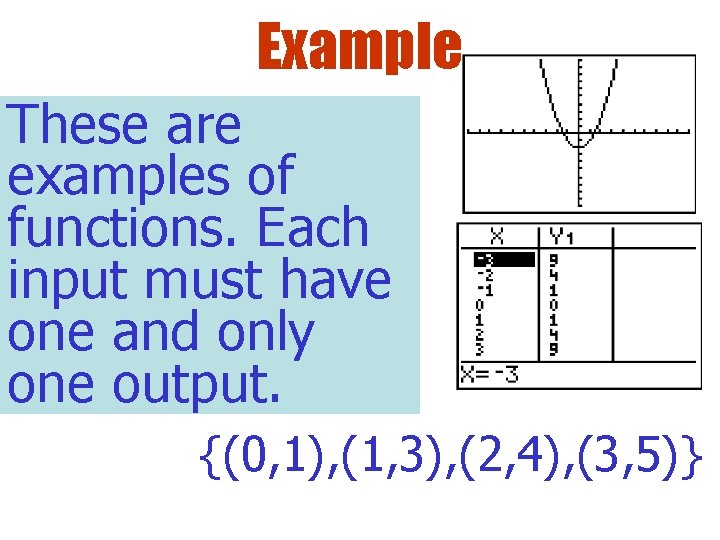
Example These are examples of functions. Each input must have one and only one output. {(0, 1), (1, 3), (2, 4), (3, 5)}

Example These are examples of relations which are not functions. Each input has more than one output. {(0, 1), (1, 3), (1, 4), (3, 5)}

Definition Function Notation: Instead of , we write If the input is 2, then the output is 7, that is : The rule is:

Try This For the function: & What is , What is the domain (inputs) and range (outputs)? D= R= is undefined

Lesson Close Without looking at your notes, define a function and give an example of something that is a function and is not a function.

Practice 1. 10/1 -13 odd 2. 11/14 -19 all Slides 1 -20 slides 21 -32 You will need a graphing calculator for many of these problems.