1 1 Properties of Real Numbers M 11

1 -1 Properties of Real Numbers M 11. A. 1. 3. 1: Locate/identify irrational numbers at the approximate location on the number line. M 11. A. 1. 3. 2: Compare and/or order any real numbers

Objectives Graphing and Ordering Real Numbers Properties of Real Numbers

Number Classification • Natural numbers are the counting numbers. • Whole numbers are natural numbers and zero. • Integers are whole numbers and their opposites. • Rational numbers can be written as a fraction. • Irrational numbers cannot be written as a fraction. • All of these numbers are real numbers.

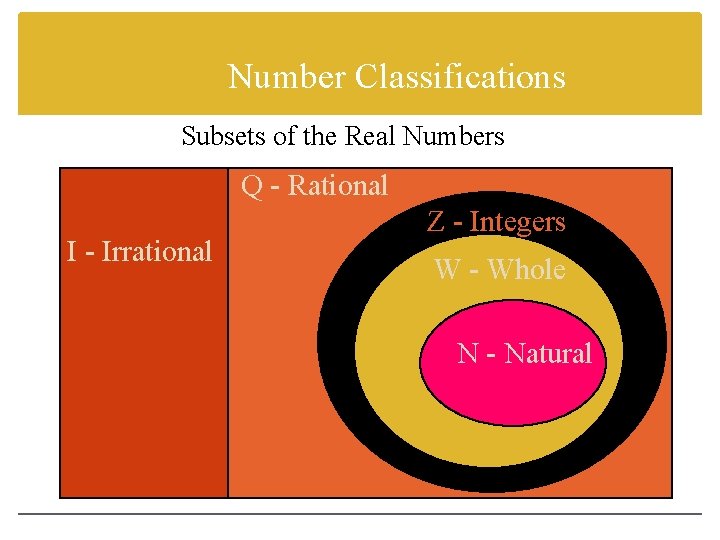
Number Classifications Subsets of the Real Numbers Q - Rational I - Irrational Z - Integers W - Whole N - Natural

Classify each number -1 6 real, rational, integer, whole, natural real, irrational real, rational 0 -2. 222 real, rational, integer, whole real, rational

Properties of Real Numbers Graph the numbers – 34 , number line. 7 , and 3. 6 on a – 34 is between – 1 and 0. Use a calculator to find that 7 2. 65. Work on Quick Check #2 on Page 6

Properties of Real Numbers Compare – 9 and – 9 = 3, so – 9. Use the symbols < and >. 9 = – 3. Since – 9 < – 3, it follows that – 9 < – 9. Work on Quick Check #3 on Page 6

Properties of Real Numbers Inverses The Additive Inverse of any number a is -a. The sum of opposites is 0. The Multiplicative Inverse of any nonzero number a is 1/a. The product of reciprocals is 1.

Properties of Real Numbers Find the opposite and the reciprocal of each number. a. – 3 17 b. 4 Opposite: –(– 3 17 Reciprocal: 1 1 – 3 7 ) = 3 17 = 1 – 22 Opposite: – 4 =– 7 22 Reciprocal: 1 7 Work on Quick Check #4 on Page 7 4

Properties of Real Numbers Commutative Property • Think… commuting to work. • Deals with ORDER. It doesn’t matter what order you ADD or MULTIPLY. • a+b = b+a • 4 • 6 = 6 • 4

Properties of Real Numbers Associative Property • Think…the people you associate with, your group. • Deals with grouping when you Add or Multiply. • Order does not change.

Properties of Real Numbers Associative Property • • (a + b) + c = a + ( b + c) (nm)p = n(mp)

Properties of Real Numbers Additive Identity Property • s + 0 = s Multiplicative Identity Property • 1(b) = b

Properties of Real Numbers Distributive Property • a(b + c) = ab + ac • (r + s)9 = 9 r + 9 s

Name the Property • 5=5+0 Additive Identity • 5(2 x + 7) = 10 x + 35 Distributive • 8 • 7=7 • 8 Commutative • 24(2) = 2(24) Commutative • (7 + 8) + 2 = 2 + (7 + 8) Commutative

Name the Property • 7 + (8 + 2) = (7 + 8) + 2 • Associative • 1 • v + -4 = v + -4 • (6 - 3 a)b = 6 b - 3 ab • 4(a + b) = 4 a + 4 b • Multiplicative Identity • Distributive

Properties of Real Numbers The absolute value of a real number is the distance from zero on the number line. Simplify | 4 13 |, |– 9. 2|, and |3 – 8|. 413 is 4 13 units from 0, so | 4 13 | = 4 13. – 9. 2 is 9. 2 units from 0, so |– 9. 2| = 9. 2. |3 – 8| = |– 5| and – 5 is 5 units from 0. So, |– 5| = 5, and hence |3 – 8| = 5. Work on Quick Check #6 on Page 8

1 -2 Algebraic Expressions M 11. A. 3. 1. 1 – Simplify/Evaluate expressions using the order of operations to solve problems

Objectives Evaluating Algebraic Expressions Simplifying Algebraic Expressions

Vocabulary A variable is a symbol, usually a letter, that represents one or more numbers. An algebraic expression is an expression that contains at least one variable. You can evaluate an algebraic expression by replacing each variable with a value and then applying the Order of Operations.

Order of Operations Parenthesis Exponents Multiply & Divide from Left to Right Add & Subtract from Left to Right

Example: Evaluate a(5 a + 2 b) if a=3 and b=-2 Substitute the values into the expression. 3[5(3) + 2(-2)] Now apply the Order of Operations: Inside the brackets, perform multiplication and division before addition and subtraction 5(3) = 15 and 2(-2)= -4 3[15 + -4] then 15 + -4 = 11 3[11] = 33

Evaluating an Algebraic Expression Evaluate 7 x – 3 xy for x = – 2 and y = 5. 7 x – 3 xy = 7(– 2) – 3(– 2) (5) Substitute – 2 for x and 5 for y. = – 14 – (– 30) Multiply first. = – 14 + 30 To subtract, add the opposite. = 16 Add. Work on Quick Check #1 on page 12

Evaluating an Algebraic Expression with Exponents Evaluate (k – 18)2 – 4 k for k = 6. (k – 18)2 – 4 k = (6 – 18)2 – 4(6) Substitute 6 for k. = (– 12)2 – 4(6) Subtract within parentheses. = 144 – 4(6) Simplify the power. = 144 – 24 Multiply. = 120 Subtract. Work on Quick Check #2 on page 12

Vocabulary Simplifying Algebraic Expressions A term is a number, a variable, or product of a number and one or more variables. The numerical factor in a term is the coefficient. Like terms have the same variables raised to the same powers. Like terms:

Combining Like Terms Simplify by combining like terms. 2 h – 3 k + 7(2 h – 3 k) = 2 h – 3 k + 14 h – 21 k Distributive Property = 2 h + 14 h – 3 k – 21 k Commutative Property = (2 + 14)h – (3 + 21)k Distributive Property = 16 h – 24 k Work on Quick Check #4 on page 14

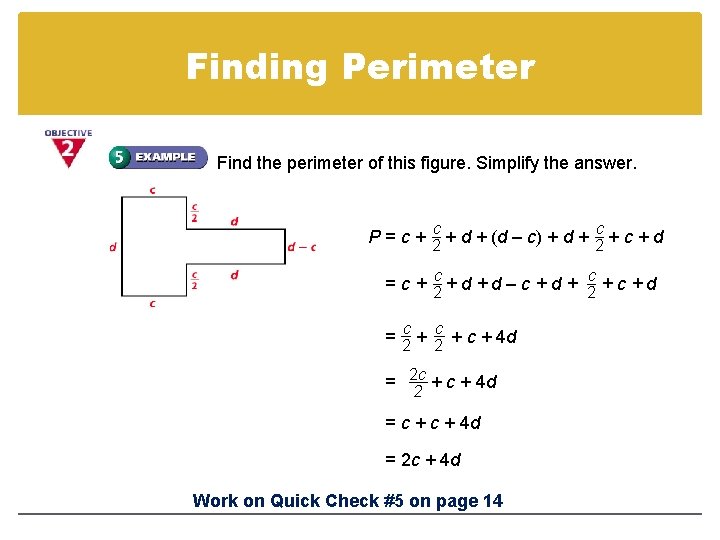
Finding Perimeter Find the perimeter of this figure. Simplify the answer. P = c + 2 c + d + (d – c) + d + 2 c + d c c = c + 2+ d – c + d + 2 + c + d c c = 2 + c + 4 d = 2 c + 4 d 2 = c + 4 d = 2 c + 4 d Work on Quick Check #5 on page 14