1 1 Captulo cuatro Descripcin de los datos

1 -1 Capítulo cuatro Descripción de los datos: medidas de dispersión OBJETIVOS Al terminar

1 -1 Capítulo cuatro continuación Descripción de datos: medidas de dispersión OBJETIVOS Al terminar

4 -3 Desviación media • Desviación media: media aritmética de los valores absolutos de

4 -4 EJEMPLO 1 • Los pesos de una muestra de cajas con libros

4 -5 Variancia de la población • La varianza de la población para datos

4 -6 EJEMPLO 2 • Las edades de la familia Dunn son 2, 18,

4 -7 Variancia poblacional continuación • Una fórmula alternativa para la variancia poblacional es:

4 -8 Desviación estándar poblacional • La desviación estándar poblacional ( ) es la

4 -9 Variancia muestral • La variancia muestral estima la variancia de la población.

4 -10 EJEMPLO 3 • Una muestra de cinco salarios por hora para varios

4 -11 Desviación estándar muestral • La desviación estándar muestral es la raíz cuadrada

4 -12 Medidas de dispersión: datos no agrupados • Para datos no agrupados, la

4 -13 Variancia muestral para datos agrupados • La fórmula de la variancia para

4 -14 Interpretación y usos de la desviación estándar • Teorema de Chebyshev: para

4 -15 Interpretación y usos de la deviación estándar • Regla empírica: para una

Curva en forma de campana que muestra la relación entre y 3 © 2001

4 -17 Dispersión relativa • El coeficiente de variación es la razón de la

4 -18 Asimetría • Asimetría (sesgo) es la medida de la falta de simetría

4 -19 Amplitud intercuartílica • La amplitud intercuartílica es la distancia entre el tercer

4 -20 Primer cuartil • El primer cuartil es el valor correspondiente al punto

4 -21 Tercer cuartil • El tercer cuartil es el valor correspondiente al punto

4 -22 Desviación cuartílica • La desviación cuartílica es la mitad de la distancia

4 -23 EJEMPLO 5 • Si el tercer cuartil = 24 y el primer

4 -24 Amplitud cuartílica • Cada conjunto de datos tiene 99 porcentiles, que dividen

4 -25 Fórmula para porcentiles © 2001 Alfaomega Grupo Editor

4 -26 Diagramas de caja • Un diagrama de caja es una ilustración gráfica,

4 -27 EJEMPLO 6 • Con base en una muestra de 20 entregas, Marco’s

4 -28 EJEMPLO 6 continuación mediana • mín Q 1 12 14 Q 3

Slides: 28

Download presentation

1 -1 Capítulo cuatro Descripción de los datos: medidas de dispersión OBJETIVOS Al terminar este capítulo podrá: UNO Calcular e interpretar la amplitud de variación, la desviación media, la variancia, y la desviación estándar de los datos originales. DOS Calcular e interpretar la amplitud de variación, la variancia y la desviación estándar de datos agrupados. TRES Explicar las características, usos, ventajas y desventajas de cada medida de dispersión. © 2001 Alfaoemega Alfaomega Grupo Gruo Editor

1 -1 Capítulo cuatro continuación Descripción de datos: medidas de dispersión OBJETIVOS Al terminar este capítulo podrá: CUATRO Entender el problema de Chebyshev y la regla normal o empírica, y su relación con un conjuto de observaciones. CINCO Calcular y explicar los cuartiles y la amplitud de variación intercuartílica. SEIS Elaborar e interpretar los diagramas de caja. SIETE Calcular y entender el coeficiente de variación y el coeficiente de asimetría. © 2001 Alfaoemega Gruo Editor Alfaomega Grupo

4 -4 EJEMPLO 1 • Los pesos de una muestra de cajas con libros en una librería son (en lb) 103, 97, 101, 106 y 103. • X = 510/5 = 102 lb • = 1 + 5 + 1 + 4 + 1 = 12 • MD = 12/5 = 2. 4 • Por lo común los pesos de las cajas están a 2. 4 lb del peso medio de 102 lb. © 2001 Alfaomega Grupo Editor

4 -5 Variancia de la población • La varianza de la población para datos no agrupados es la media aritmética de las desviaciones cuadráticas respecto a la media de la población. © 2001 Alfaomega Grupo Editor

4 -8 Desviación estándar poblacional • La desviación estándar poblacional ( ) es la raíz cuadrada de la variancia de la población. • Para el EJEMPLO 2, la desviación estándar poblacional es 15. 19 (raíz cuadrada de 230. 81). © 2001 Alfaomega Grupo Editor

4 -10 EJEMPLO 3 • Una muestra de cinco salarios por hora para varios trabajos en el área es: $7, $5, $11, $8, $6. Encuentre la variancia. • X = 37/5 = 7. 40 • = 21. 2/(5 -1) = 5. 3 © 2001 Alfaomega Grupo Editor

4 -11 Desviación estándar muestral • La desviación estándar muestral es la raíz cuadrada de la variancia muestral. • En el EJEMPLO 3, la desviación estándar de la muestra es = 2. 30 © 2001 Alfaomega Grupo Editor

4 -12 Medidas de dispersión: datos no agrupados • Para datos no agrupados, la amplitud es la diferencia entre los valores mayor y menor en un conjunto de datos. • AMPLITUD = valor mayor - valor menor • EJEMPLO 4: una muestra de cinco graduados de contaduría indicó los siguientes salarios iniciales: $22 000, $28 000, $31 000, $23 000, $24 000. La amplitud es $31 000 $22 000 = $9 000. © 2001 Alfaomega Grupo Editor

4 -13 Variancia muestral para datos agrupados • La fórmula de la variancia para datos agrupados usada como estimador de la vaiancia poblacional es: • donde f es la frecuencia de clase y X es el punto medio de la clase. © 2001 Alfaomega Grupo Editor

4 -14 Interpretación y usos de la desviación estándar • Teorema de Chebyshev: para cualquier conjunto de observaciones, la proporción mínima de valores que está dentro de k desviaciones estándar desde la media es al menos 1 - 1/k , donde k 2 es una constante mayor que 1. © 2001 Alfaomega Grupo Editor

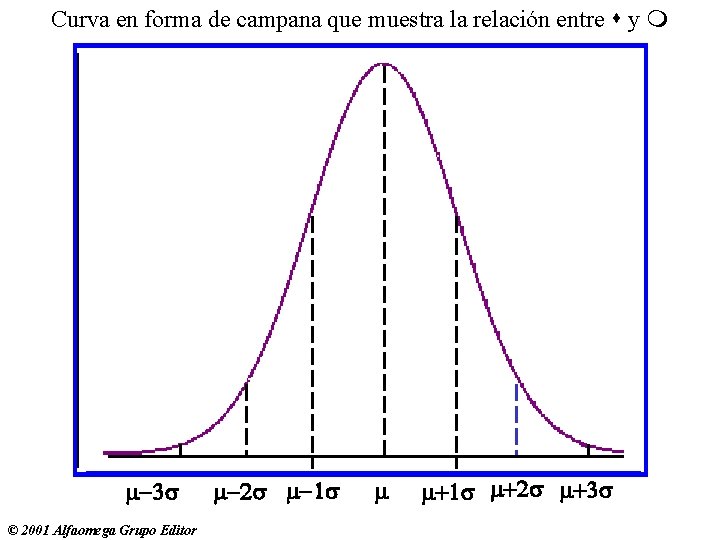
4 -15 Interpretación y usos de la deviación estándar • Regla empírica: para una distribución de frecuencias simétrica de campana, cerca de 68% de las observaciones estará dentro de ± 1 de la media ( ); cerca de 95% de las observaciones estará dentro de ± 2 de la media ( ); alrededor de 99. 7% estará dentro de ± 3 de la media ( ). © 2001 Alfaomega Grupo Editor

4 -18 Asimetría • Asimetría (sesgo) es la medida de la falta de simetría en una distribución. • El coeficiente de asimetría se calcula mediante la siguiente fórmula: Sk 3(media - mediana) = desviación estándar © 2001 Alfaomega Grupo Editor

4 -19 Amplitud intercuartílica • La amplitud intercuartílica es la distancia entre el tercer cuartil Q 3 y el primer cuartil Q 1. • Amplitud intercuartílica = tercer cuartil - primer cuartil = Q 3 - Q 1 © 2001 Alfaomega Grupo Editor

4 -20 Primer cuartil • El primer cuartil es el valor correspondiente al punto debajo del cual se encuentra el 25% de las observaciones en un conjunto ordenado de datos. • donde L = límite de las clasese que contienen Q 1, CF = frecuencia acumulda que precede a la clase que contiene a Q 1, f = frecuencia de la clase que contiene Q 1, i= tamaño de la clase que contiene Q 1. © 2001 Alfaomega Grupo Editor

4 -21 Tercer cuartil • El tercer cuartil es el valor correspondiente al punto debajo del cual se encuentra 75% de las observaciones en un conjunto ordenado de datos: donde L = límite inferior de la clase que contiene a Q 3, CF = frecuencia acumulada precedente a la clase que contiene a Q 3, f = frequencia de la clase que contiene a Q 3, i = tamaño de la clase que contiene a Q 3. © 2001 Alfaomega Grupo Editor

4 -23 EJEMPLO 5 • Si el tercer cuartil = 24 y el primer cuartil = 10, ¿cuál es la desviación cuartílica? La amplitud intercuartílica es 24 - 10 = 14; por lo tanto, la desviación cuartílica es 14/2 = 7. © 2001 Alfaomega Grupo Editor

4 -24 Amplitud cuartílica • Cada conjunto de datos tiene 99 porcentiles, que dividen el conjunto en 100 partes iguales. • La amplitud cuartílica es la distancia entre dos porcentiles establecidos. La amplitud cuartílica 10 a 90 es la distancia entre el 10º y 90º porcentiles. © 2001 Alfaomega Grupo Editor

4 -26 Diagramas de caja • Un diagrama de caja es una ilustración gráfica, basada en cuartiles, que ayuda a visualizar un conjunto de datos. • Se requieren cinco tipos de datos para construir un diagrama de caja: el valor mínimo, el primer cuartil, la mediana, el tercer cuartil, y el valor máximo. © 2001 Alfaomega Grupo Editor

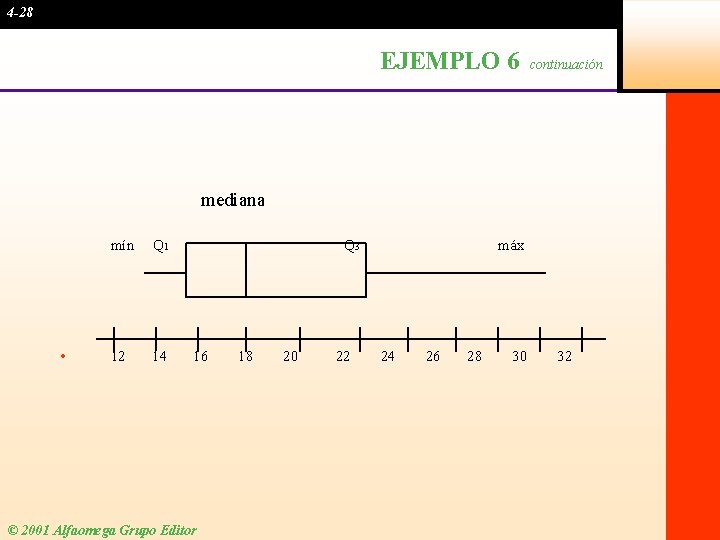
4 -27 EJEMPLO 6 • Con base en una muestra de 20 entregas, Marco’s Pizza determinó la siguiente información: valor mínimo = 13 minutos, Q 1 = 15 minutos, mediana = 18 minutos, Q 3 = 22 minutos, valor máximo = 30 minutos. Desarrolle un diagrama de caja para los tiempos de entrega. © 2001 Alfaomega Grupo Editor