1 1 5 Linear Operators Christopher Crawford PHY

§ 1. 1. 5 Linear Operators Christopher Crawford PHY 311 2014 -01 -17

Outline • Linear operators Characterization – matrices/tensors • • Change of basis – coordinate transform of vectors Active vs. passive rotations Basis vs. components – `contravariant’ components Properties of orthogonal transformations • Eigenparaphernalia Eigen-{vectors, values, spaces} Similarity transform – coordinate transform of matrices Properties of Hermitian (symmetric) operators • Polar decomposition – put it all together! Exponential map, symmetry Singular value decomposition (SVD) 2

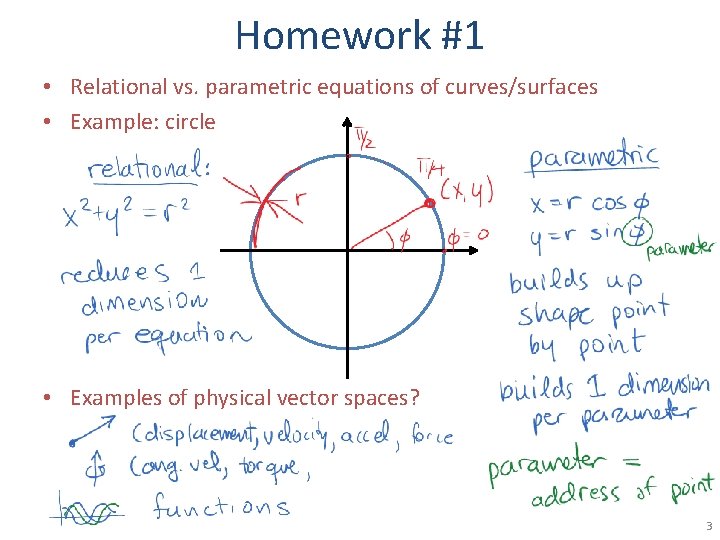
Homework #1 • Relational vs. parametric equations of curves/surfaces • Example: circle • Examples of physical vector spaces? 3

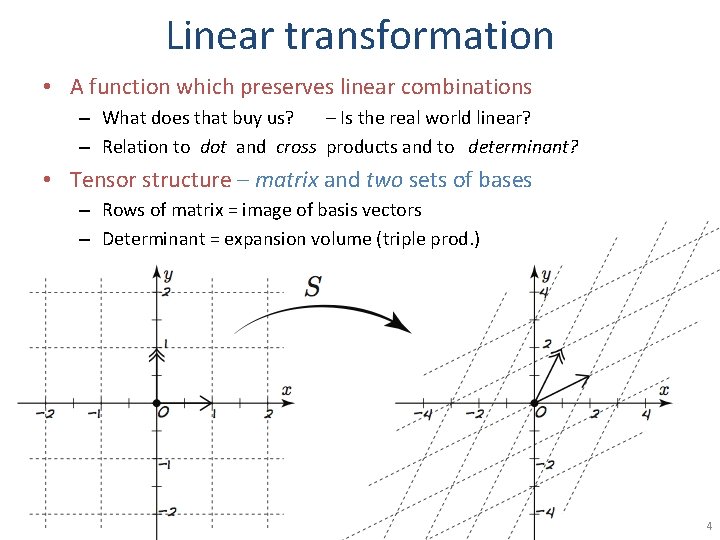
Linear transformation • A function which preserves linear combinations – What does that buy us? – Is the real world linear? – Relation to dot and cross products and to determinant? • Tensor structure – matrix and two sets of bases – Rows of matrix = image of basis vectors – Determinant = expansion volume (triple prod. ) 4

Change of coordinates • Two ways of thinking about transformations – Both yield the same rotation matrix! Difference is in what you rotate. ACTIVE PASSIVE – Single basis fixed – Actively rotate vector – Easier to calculate matrix? – Physical vector still (passive) – Rotate basis vectors – Easier to compose rotations? EXAMPLE: 2 -d rotation 5

Passive transform: basis/components • What is the meaning of `contravariant components’? 6

Passive transform: basis/components • What is the meaning of `contravariant components’? • Example: simple rotation 7

Orthogonal transformations • R is orthogonal (rotation) if it `preserves the metric’ (distances and angles are the same before and after • Development in terms of basis: 8

Orthogonal transformations • R is orthogonal (rotation) if it `preserves the metric’ (distances and angles are the same before and after • Development in terms of basis: 9

Orthogonal transformations • R is orthogonal (rotation) if it `preserves the metric’ (distances and angles are the same before and after • Development in terms of basis: • Development in terms of components: 10

Orthogonal transformations • R is orthogonal (rotation) if it `preserves the metric’ (distances and angles are the same before and after • Development in terms of basis: • Development in terms of components: • Starting with an orthonormal basis: 11

Illustration of Eigenspace • Symmetric matrix S with eigenvectors vi , eigenvalues λi • Similarity transform – change of basis to diagonalize S 12

Properties of symmetric matrices • A symmetric (Hermitian) matrix has real eigenvalues – What about an antisymmetric / orthogonal matrix? • Eigenvectors of a symmetric (Hermitian) matrix with distinct eigenvalues are orthogonal 13

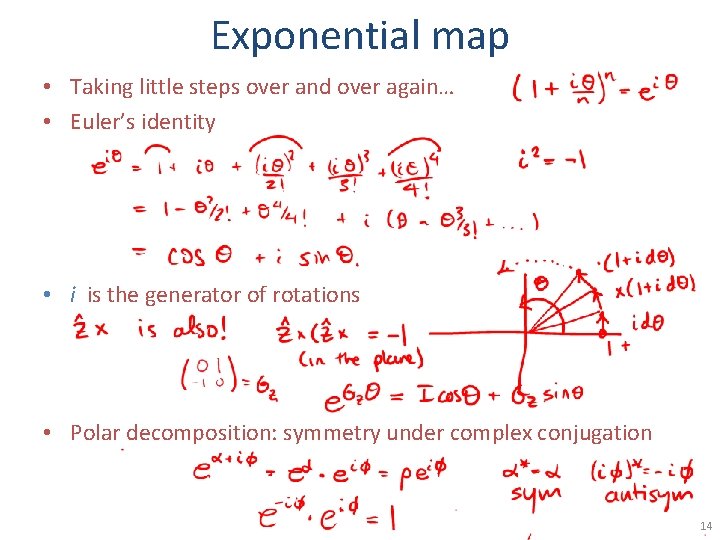
Exponential map • Taking little steps over and over again… • Euler’s identity • i is the generator of rotations • Polar decomposition: symmetry under complex conjugation 14

Polar decomposition • Apply the same principle from complex numbers to operators • Not quite so clean due to noncommutativity of matrices • This is the basic example of a `Lie algebra’ 15

Singular value decomposition (SVD) • Breaks down the structure of any m x n matrix into rotations, a stretch and a projection • Extremely useful in numerical routines 16