1 01 10 1 01 01 How Computers

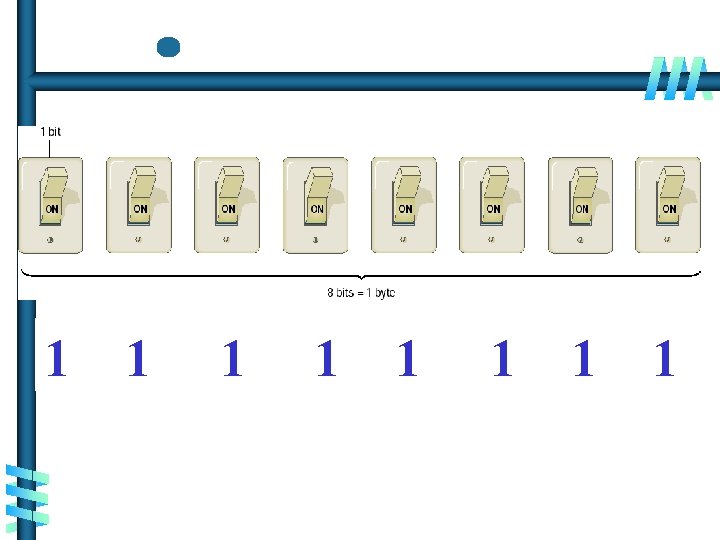
1 01 10 1 01 01

How Computers Represent Data - Text Codes • A text code is a system that uses binary numbers (1 s and 0 s) to represent characters understood by humans (letters and numerals). • An early text code system, called EBCDIC, uses eightbit codes, but is used primarily in older mainframe systems. • In the most common text-code set, ASCII, each character consists of eight bits (one byte) of data. ASCII is used in nearly all personal computers. • In the Unicode text-code set, each character consists of 16 bits (two bytes) of data.

Text Codes Examples from the ASCII Text Code Character 00110000 0 00110001 1 00110010 2 0011 3 00110100 4 00110101 5 01000001 A 01000010 B 01000011 C 0100 D 01000101 E

Goal: Representing Numbers in Binary b Base 10 (decimal) - Numbers are represented using 10 numerals: 0, 1, 2, 3 … 9 b Base 2 (binary) - Numbers are represented using 2 numerals: 0, 1 b Base 10 - Each position represents a power of 10: 101 = 1*102 + 0*101 + 1*100 = 100 + 1 110 = 1*102 + 1*101 + 0*100 = 100 + 10 b Base 2 - Each position represents a power of 2: 101 b = 1*22 + 0*21 + 1*20 = 100 b + 1 b = 4 + 1 110 b = 1*22 + 1*21 + 0*20 = 100 b + 10 b = 4+2

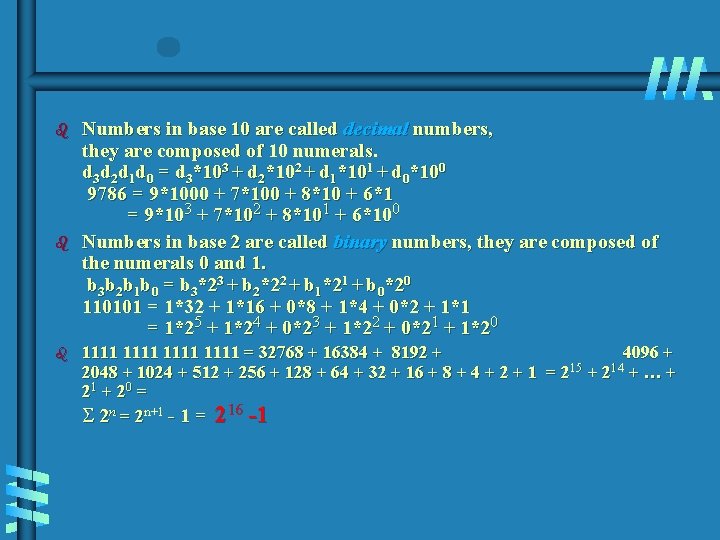
b b b Numbers in base 10 are called decimal numbers, they are composed of 10 numerals. d 3 d 2 d 1 d 0 = d 3*103 + d 2*102 + d 1*101 + d 0*100 9786 = 9*1000 + 7*100 + 8*10 + 6*1 = 9*103 + 7*102 + 8*101 + 6*100 Numbers in base 2 are called binary numbers, they are composed of the numerals 0 and 1. b 3 b 2 b 1 b 0 = b 3*23 + b 2*22 + b 1*21 + b 0*20 110101 = 1*32 + 1*16 + 0*8 + 1*4 + 0*2 + 1*1 = 1*25 + 1*24 + 0*23 + 1*22 + 0*21 + 1*20 1111 = 32768 + 16384 + 8192 + 4096 + 15 14 2048 + 1024 + 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 2 + … + 21 + 20 = S 2 n = 2 n+1 - 1 = 216 -1

Converting from Binary to Decimal b b Easy: Multiply each numeral by its exponent. 1001 b = 1*23 + 1*20 = 1*8 + 1*1 = 9 d 0111 b = 0*23 + 1*22 + 1*21 + 1*20 = 100 b + 1 b =4+2+1 =7 110110 b = 1*25 + 1*24 + 0*23 + 1*22 + 1*21 = 100000 b + 100 b + 10 b = 32 + 16 + 4 + 2 = 54

Converting from Binary to Decimal b Given an array that holds a 32 digit binary number called binary: b int[] binary = {1, 0, 0, 1}; int decimal = 0; for(int i=binary. length-1; i>=0; i--) decimal += binary[i]*Math. pow(2, i); b The powers of 2: 20 = 1 21 = 2 24 = 16 25 = 32 28 = 256 29 = 512 211 = 2048 212 = 4096 216 = 65536 22 = 4 23 = 8 26 = 64 27 = 128 210 = 1024 = 1 K 213 = 8192 220 = 1048576 = 1 M

Converting From Decimal to Binary In Java it looks like this: int decimal = read. Int(); int res; int power; for(int n=31; n>=0; n--){ power = (int)Math. pow(2, n); res = decimal/power; decimal = decimal - res*power; System. out. print(res); }

A Base Conversion Example 500/29 = 0 ; 500 - 0 = 500/28 = 1 ; 500 - 256 = 244/27 = 1 ; 244 - 128 = 116/26 = 1 ; 116 - 64 = 52 52/25 = 1 ; 52 - 32 = 20 20/24 = 1 ; 20 - 16 = 4 500 d = 111110100 b 4/23 4/22 0/21 0/20 =0; 4 -0= =1; 4 -4= =0; 0 -0= 4 0 0 0

Representation of Numbers b int, long, short, char - positive numbers are stored as a binary number where the MSB (Most Significant Bit) is 0 A short is represented by 16 bits (2 bytes) 100 d = 26 + 25 + 22 = 000001100100 An int is represented by 32 bits (4 bytes) 65545 d = 216 + 23 + 20 = 0000000010000001001 A char is represented by 16 bits (2 bytes) ‘ 0’ = 48 d = 25 + 24 =0000 00110000

Signed and Unsigned Numbers b b b How do we distinguish between them? Solution: Use 1 bit to represents the sign. The name of this scheme is called: sign and magnitude 00011111 b = -15 00001111 b = +15 (8 bit numbers) There are several problems with this scheme: • where do we put the sign? • an extra step is needed to calculate the sign bit – Add the magnitudes. – Calculate the sign. • there is both a positive and negative zero 00000001 b = -0 0000 b = +0

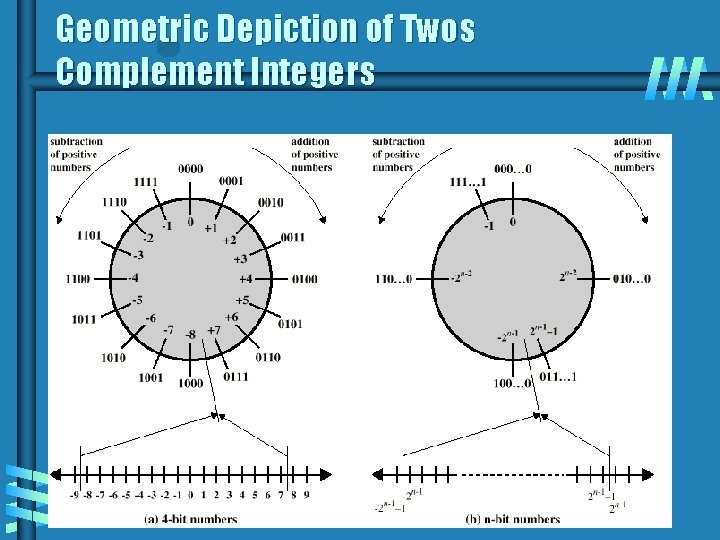
Two's Complement b b b New Solution: Leading 0 s mean positive and leading 1 s mean negative. 01111111 b > 0 10000000 b < 0 (8 bit numbers) The largest positive number is: 2, 147, 483, 647 d (231 -1) = 01111… 11111 b The smallest negative number is: -2, 147, 483, 648 d (-231) = 10000… 00000 b It is followed by -2, 147, 483, 647 d (1000… 0001 b) up to -1 (1111… 1111 b). The sum of a number and its inverse is 100. . . 0, where 1 is an overflow and is thrown away.

Two’s Complement b b b b +3 = 00000011 +2 = 00000010 +1 = 00000001 +0 = 0000 -1 = 1111 -2 = 11111110 -3 = 11111101

Benefits b b b One representation of zero Arithmetic works easily (see later) Negating is fairly easy • • • 3 = 00000011 Boolean complement gives 11111100 Add 1 to LSB 11111101

Geometric Depiction of Twos Complement Integers

Negative Decimal to Binary b b b Translate the number to binary. Flip the bits (1 -> 0, 0 -> 1) Add 1 b b -100 d = -01100100 = 10011011 + 1 = 10011100 -1 d = - 00000001 = 11111110 + 1 = 1111 b -128 d = -10000000 = 01111111 + 1 = 10000000 b 11000101 b = 00111010 + 1 = 00111011 = -59 d In a short: -25, 000 d = -0110000110101000 = 1001111001010111 + 1 = 1001111000 b

Conversion Between Lengths b b b b Positive numbers pack with leading zeros +18 = 00010010 +18 = 0000 00010010 Negative numbers pack with leading ones -18 = 10010010 -18 = 1111 10010010 i. e. pack with MSB (sign bit)

Hexadecimal Numbers b Numbers in base 16 are called hexadecimal numbers, they are composed of 16 numerals (0 -9, a-f). 9786 hex = = 016*6 + 116*8 + 216*7 + 316*9 38790 = 1*6 + 16*8 + 256*7 + 4096*9 = d + 2 3 4 5 0 xabcdef = 16*13 + 16*12 + 16*11 + 16*10 11259375 = 016*15 + 116*14 d b The conversion from binary to hex is very easy, each hex digit is 4 binary digits: 0 x 0 = 0000 0 x 1 = 0001 0 x 2 = 0010 0 x 3 = 0011 0 x 4 = 0100 0 x 5 = 0101 0 x 6 = 0110 0 x 7 = 0111 0 x 8 = 1000 0 x 9 = 1001 0 xa = 1010 0 xb = 1011 0 xc = 1100 0 xd = 1101 0 xe = 1110 0 xf = 1111

Binary <-> Hexadecimal b b Using the previous table it is easy to represent 32 bit binary numbers in a short form: 0100 1010 0010 1101 1000 1100 0111 1001 = 4 a 2 d 8 c 7 9 = 0 x 4 a 2 d 8 c 79. 0 x 12390 ab 4 = 0001 0010 0011 1001 0000 1011 0100 1 2 3 9 0 a b 4 0 xffff = 1111 1111 Every 2 Hex digits are a byte

Decimal -> Hexadecimal b Conversion from decimal to hexadecimal is similar to converting decimal to binary. int decimal=read. Int(); int res; int power; for(int n=7; n>=0; n--){ power = (int)Math. pow(16, n); res = decimal/power; decimal = decimal - res*power; if(res>9) System. out. print((char)((res - 10) + 'a')); else System. out. print(res); }

Octal & Hex in Java b Java allows numbers in octal (start with 0) and hexadecimal (start with 0 x or 0 X). int num 1 = 015; int num 2 = 0 x 1 a; num 1 is 13 num 2 is 26

Addition b Lets add 6 to 7: 00… 00111 = 7 d 00… 00110 = 6 d 00… 01101 = 13 d b Lets add 11 to 5: 00… 01011 = 11 d 00… 00101 = 5 d 00… 10000 = 16 d

Substraction b Subtraction uses addition, the operand is simply negated before being added: 7 - 6 = 7 + (-6) = 00… 00111 = 7 d 11… 11010 = -6 d 00… 00001 = 1 d

Overflow b Overflow occurs when the result of a operation can't be represented by the hardware. This can happen when we add two numbers of the same sign or subtract two large numbers of opposing signs. b Overflow is detected by the following table: Operation A+B A- B A B >=0 <0 <0 >=0 Result <0 >=0

Multiplication b Look at the following pencil and paper example: X b 1000 d 1001 d 1000 0000 1001000 d By restricting the digits to 1 & 0 (which is binary) the algorithm is simple, at each step: • • • Place a copy of the multiplicand if the multiplier digit is 1. Place 0 if the digit is 0. The position for the next step is shifted left by one place.

Real Numbers b b Numbers with fractions Could be done in pure binary • 1001. 1010 = 24 + 20 +2 -1 + 2 -3 =9. 625 b b Where is the binary point? Fixed? • Very limited b Moving? • How do you show where it is?

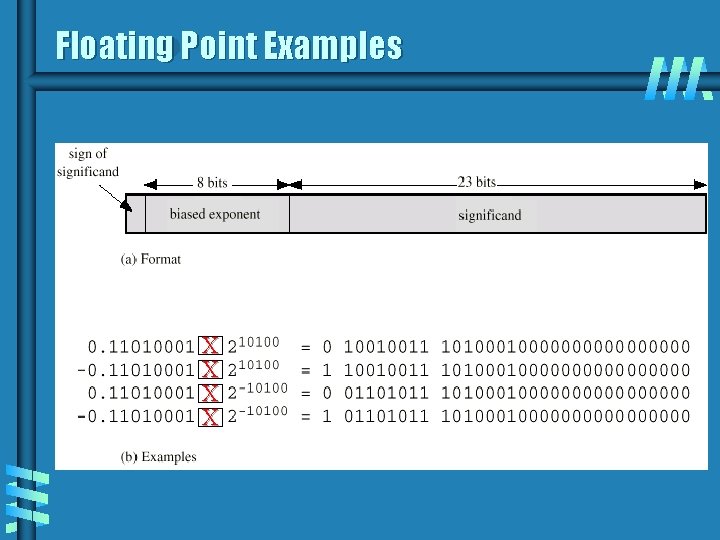
Sign bit Floating Point b b b Biased Exponent Significand or Mantissa +/-. significand x 2 exponent Point is actually fixed between sign bit and body of mantissa Exponent indicates place value (point position)

Signs for Floating Point b b Mantissa is stored in 2 s compliment Exponent is in excess or biased notation • • • e. g. Excess (bias) 128 means 8 bit exponent field Pure value range 0 -255 Subtract 128 to get correct value Range -128 to +127

Normalization b b b FP numbers are usually normalized i. e. exponent is adjusted so that leading bit (MSB) of mantissa is 1 Since it is always 1 there is no need to store it (c. f. Scientific notation where numbers are normalized to give a single digit before the decimal point e. g. 3. 123 x 103)

Floating Point Examples X X

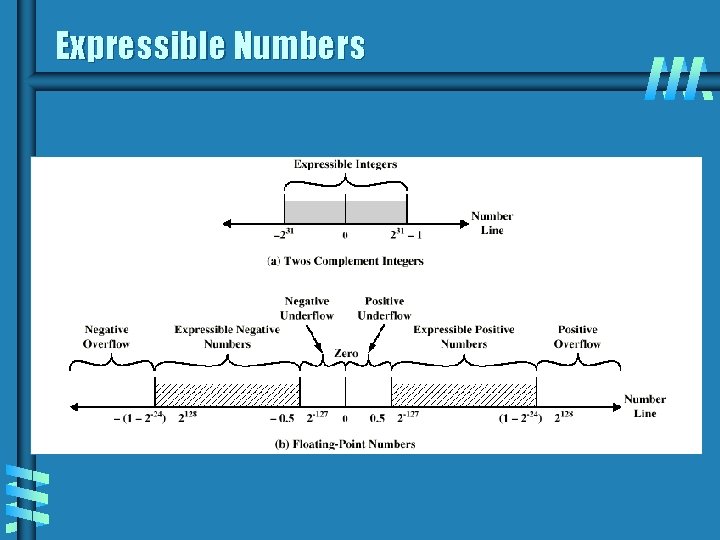
Expressible Numbers

IEEE 754 b b Standard for floating point storage 32 and 64 bit standards 8 and 11 bit exponent respectively Extended formats (both mantissa and exponent) for intermediate results

FP Arithmetic +/- b b Check for zeros Align significands (adjusting exponents) Add or subtract significands Normalize result

FP Arithmetic x/ b b b Check for zero Add/subtract exponents Multiply/divide significands (watch sign) Normalize Round All intermediate results should be in double length storage