07122020 Mechanics 07122020 Distance Speed and Time revision






























































































- Slides: 162

07/12/2020 Mechanics

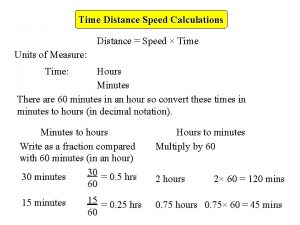
07/12/2020 Distance, Speed and Time revision Speed = distance (in metres) time (in seconds) D S T 1) Ben walks 200 metres in 40 seconds. What is his speed? 2) Alex covers 2 km in 1, 000 seconds. What is his speed? 3) How long would it take Connor to run 100 metres if he could run at 12 ms-1? 4) Dan throws a book at Adam and it travels at 50 ms-1 for 0. 2 s. How far away was Adam? 5) Katie is learning to drive. She drives her car at 85 mph (about 40 ms-1). How long does it take her to drive 20 km?

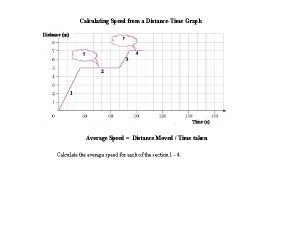
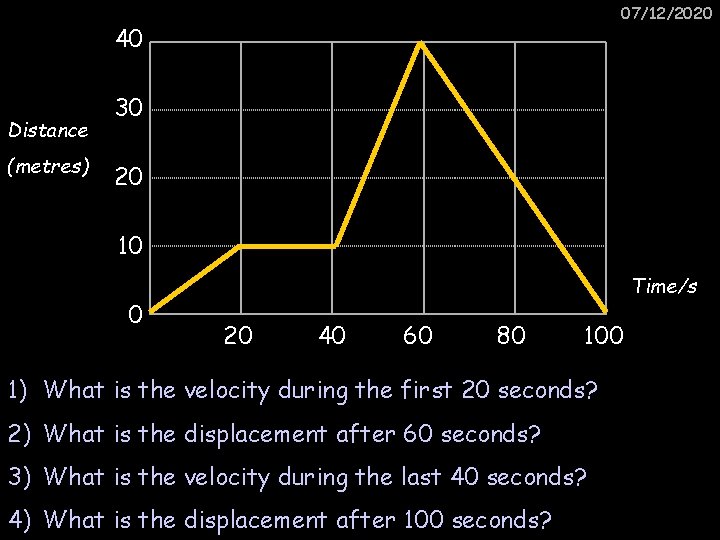
07/12/2020 40 Distance (metres) 30 20 10 0 Time/s 20 40 60 80 100 1) What is the velocity during the first 20 seconds? 2) What is the displacement after 60 seconds? 3) What is the velocity during the last 40 seconds? 4) What is the displacement after 100 seconds?

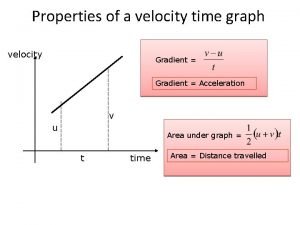
07/12/2020 Acceleration recap V-U Acceleration = change in velocity (in ms-1) (in ms-2) time taken (in s) A T 1) Ollie accelerates on his bike from 0 to 10 ms-1 in 5 seconds. What is his acceleration? 2) Danny drops a ball on his foot and it accelerates downwards at a rate of 10 ms-2 for 12 seconds. What speed did it reach? 3) A car accelerates from 10 to 20 ms-1 with an acceleration of 2 ms-2. How long did this take? 4) A rocket accelerates from 1, 000 ms-1 at a rate of 20 ms-2 for 2 minutes. What speed did it reach?

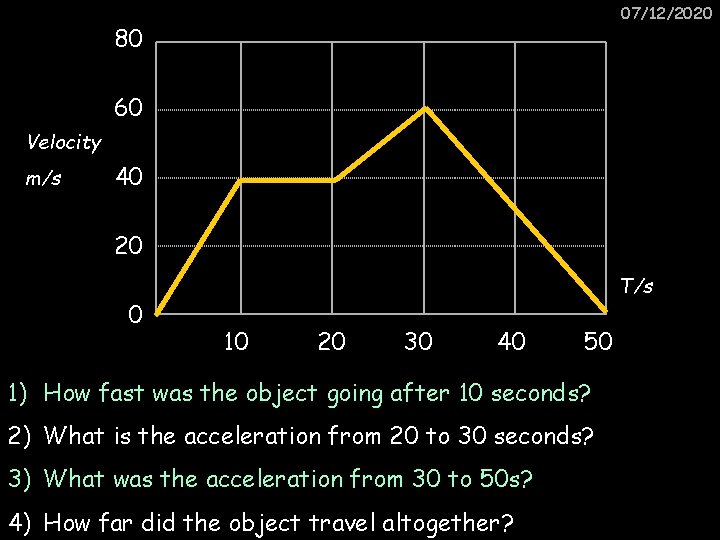
07/12/2020 80 60 Velocity m/s 40 20 0 T/s 10 20 30 40 50 1) How fast was the object going after 10 seconds? 2) What is the acceleration from 20 to 30 seconds? 3) What was the acceleration from 30 to 50 s? 4) How far did the object travel altogether?

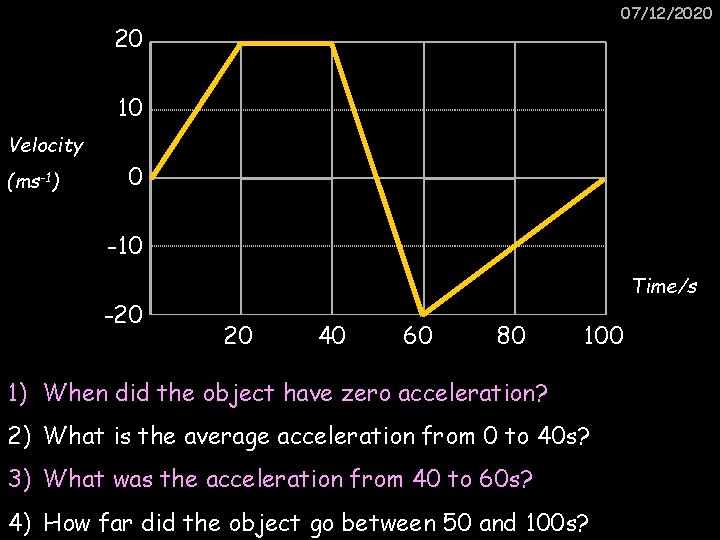
07/12/2020 20 10 Velocity (ms-1) 0 -10 -20 Time/s 20 40 60 80 100 1) When did the object have zero acceleration? 2) What is the average acceleration from 0 to 40 s? 3) What was the acceleration from 40 to 60 s? 4) How far did the object go between 50 and 100 s?

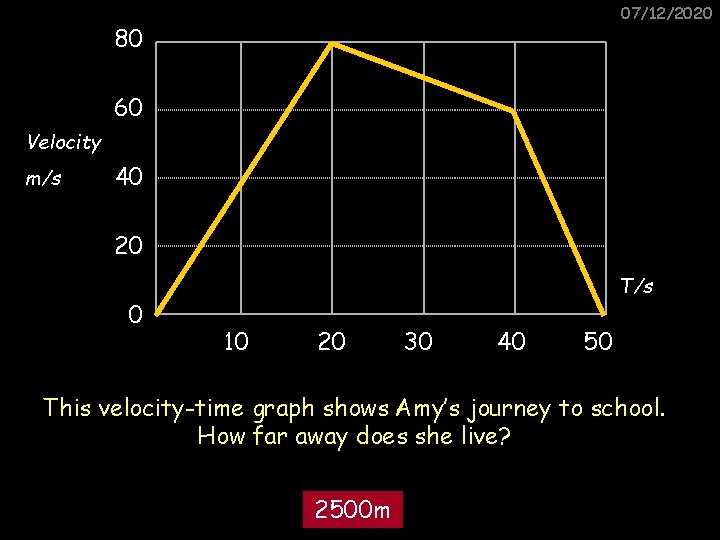
07/12/2020 80 60 Velocity m/s 40 20 0 T/s 10 20 30 40 50 This velocity-time graph shows Amy’s journey to school. How far away does she live? 2500 m

Equations of Motion 07/12/2020 u+v s= 2 t v = u + at s = ut + ½at 2 v 2 = u 2 + 2 as They’re golden!

Example questions 07/12/2020 1) Will drops a ball on Connor’s foot. How long does the ball take to fall 1 m? 2 m? Why is the second answer not simply twice the first? 2) Ed flies to Belgium. His aeroplane has a maximum acceleration on the ground of 3. 4 ms-2. What is the minimum length of runway needed to reach its take off speed of 110 ms-1 and how long will this take? 3) Danny likes watching kangaroos. A kangaroo jumps to a vertical height of 2. 8 m. For how long was it in the air? 4) Charlie likes baseball. A baseball pitcher can release a ball at 40 ms-1 after accelerating through a distance of 2. 5 m. Calculate the average acceleration of the ball.

Example questions 07/12/2020 5) Henry has a good chance of surviving a car crash with a seatbelt on if her deceleration does not exceed 30 g (30 x 9. 81 ms-2). Calculate the distance by which the front end of the car must collapse in if a crash occurs at 70 mph. 6) Joey travels in a rocket powered sledge and accelerates from rest to 284 ms-1 in 5 s and then comes to a rest in 1. 5 s. Calculate his acceleration in both stages. 7) Dan wants to play with the air track. The air track is slightly tilted. He pushes a trolley up the track with a speed of 1 ms-1 and its acceleration due to the tilt is 0. 5 ms-2 down the track. How long does it take to drop 1 m below the starting point?

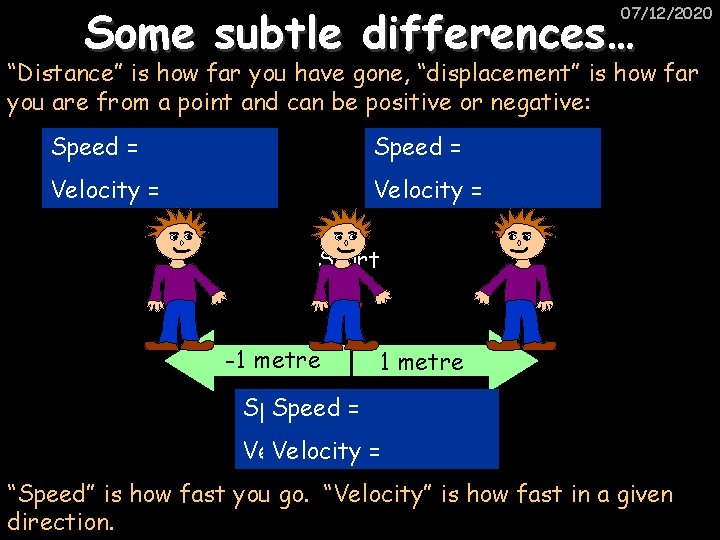
Some subtle differences… 07/12/2020 “Distance” is how far you have gone, “displacement” is how far you are from a point and can be positive or negative: Distance = Displacement = Start -1 metre Distance = = Displacement = =

Some subtle differences… 07/12/2020 “Distance” is how far you have gone, “displacement” is how far you are from a point and can be positive or negative: Speed = Velocity = Start -1 metre Speed = = Velocity = = “Speed” is how fast you go. “Velocity” is how fast in a given direction.

Vector vs. scalar 07/12/2020 Scalar quantities have size (“magnitude”) only and no direction. Vector quantities have both size and direction. Scalar or vector? ? ? Scalar Vector 8. Power 2. Distance 12. Acceleration 1. Mass 6. Energy 7. Time 3. Displacement 4. Speed 11. Force 10. Current 5. Velocity 9. Momentum

Understanding Velocity 1) Is this car travelling at constant speed? 2) Is this car travelling at constant velocity? 07/12/2020

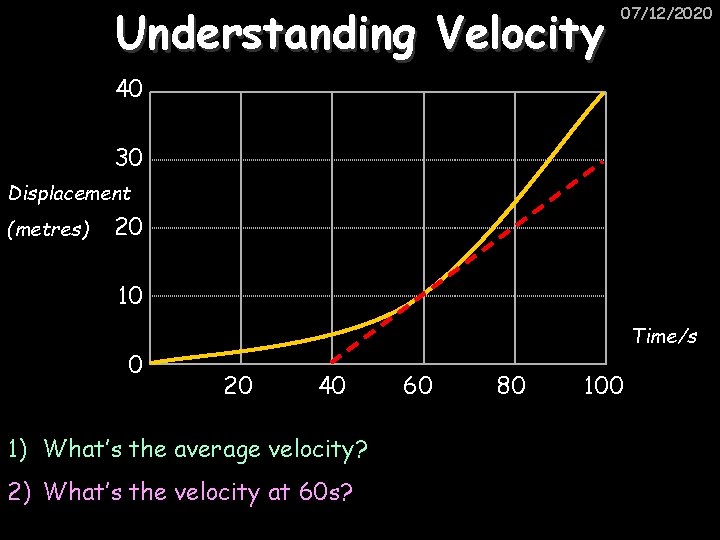
Understanding Velocity 07/12/2020 40 30 Displacement (metres) 20 10 0 Time/s 20 40 1) What’s the average velocity? 2) What’s the velocity at 60 s? 60 80 100

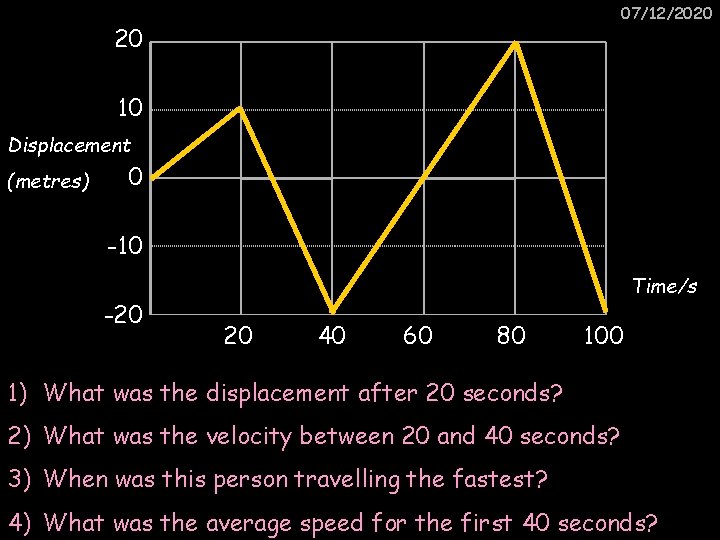
07/12/2020 20 10 Displacement (metres) 0 -10 -20 Time/s 20 40 60 80 100 1) What was the displacement after 20 seconds? 2) What was the velocity between 20 and 40 seconds? 3) When was this person travelling the fastest? 4) What was the average speed for the first 40 seconds?

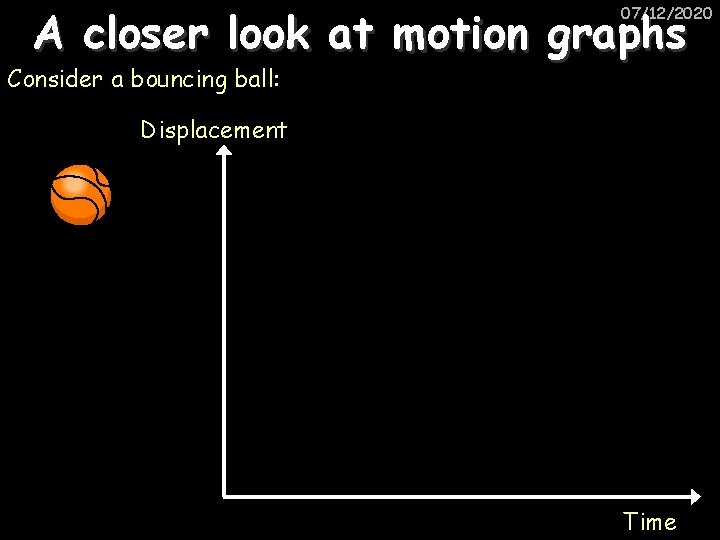
A closer look at motion graphs 07/12/2020 Consider a bouncing ball: Displacement Time

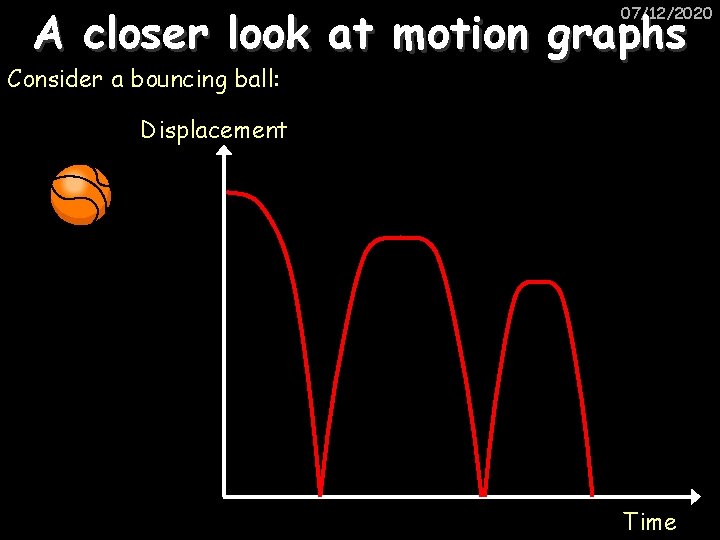
A closer look at motion graphs 07/12/2020 Consider a bouncing ball: Displacement Time

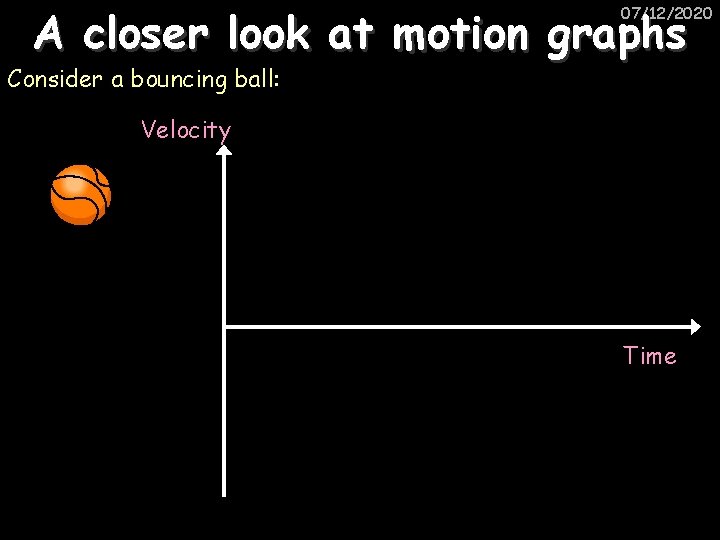
A closer look at motion graphs 07/12/2020 Consider a bouncing ball: Velocity Time

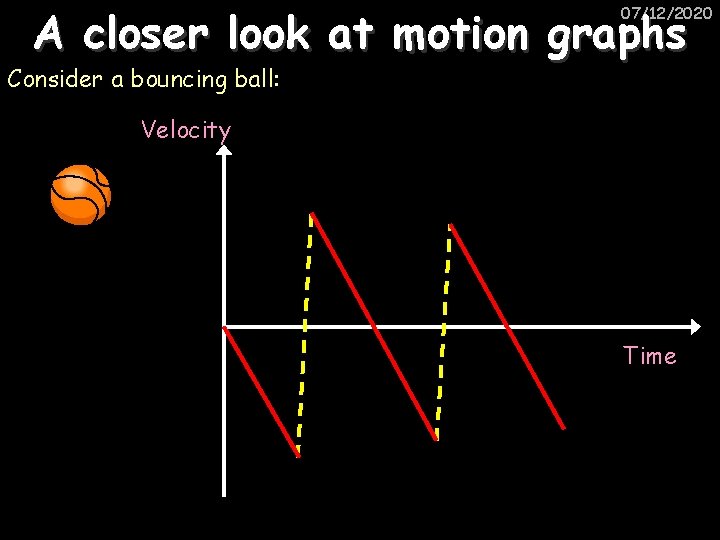
A closer look at motion graphs 07/12/2020 Consider a bouncing ball: Velocity Time

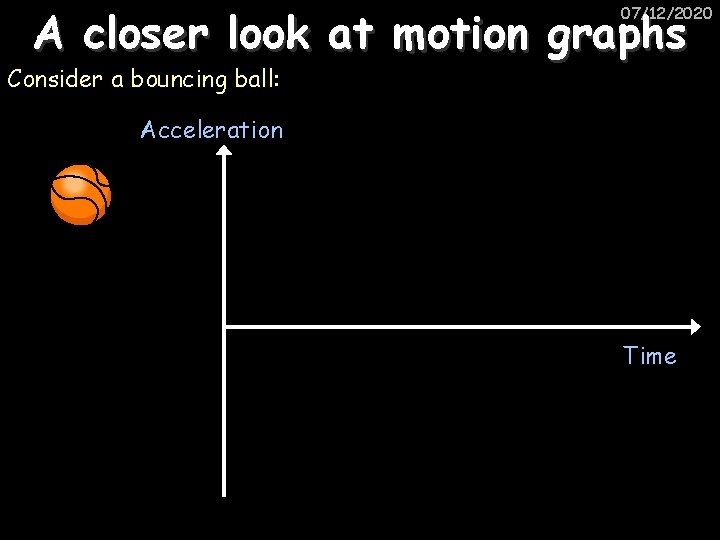
A closer look at motion graphs 07/12/2020 Consider a bouncing ball: Acceleration Time

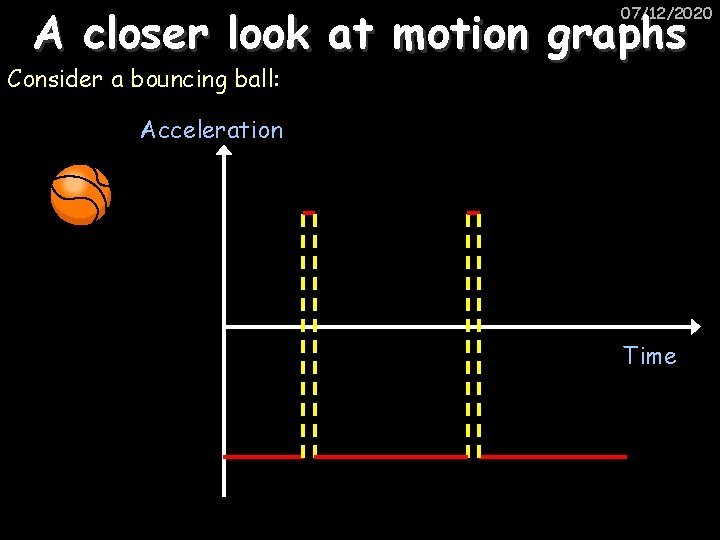
A closer look at motion graphs 07/12/2020 Consider a bouncing ball: Acceleration Time

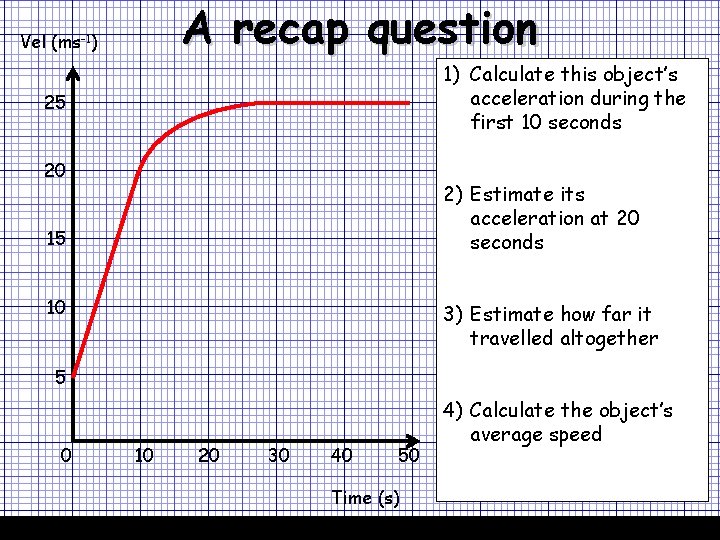
A recap question Vel (ms-1) 07/12/2020 1) Calculate this object’s acceleration during the first 10 seconds 25 20 2) Estimate its acceleration at 20 seconds 15 10 3) Estimate how far it travelled altogether 5 0 10 20 30 40 50 Time (s) 4) Calculate the object’s average speed

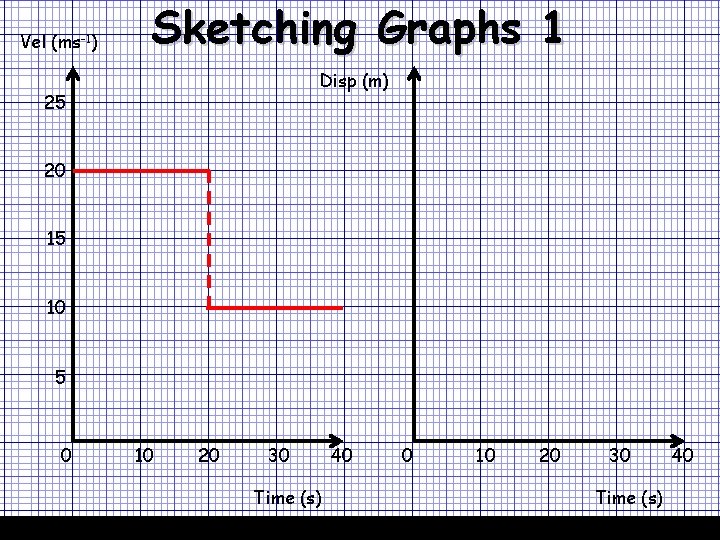
Vel (ms-1) Sketching Graphs 1 07/12/2020 Disp (m) 25 20 15 10 5 0 10 20 30 Time (s) 40

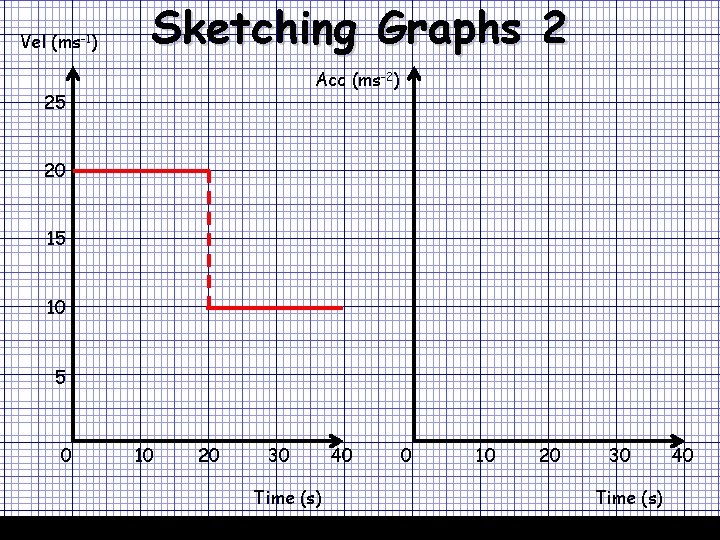
Vel (ms-1) Sketching Graphs 2 07/12/2020 Acc (ms-2) 25 20 15 10 5 0 10 20 30 Time (s) 40

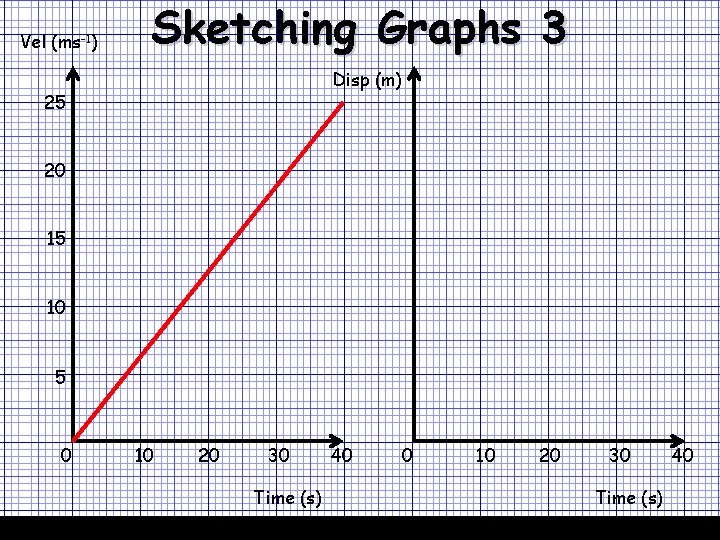
Vel (ms-1) Sketching Graphs 3 07/12/2020 Disp (m) 25 20 15 10 5 0 10 20 30 Time (s) 40

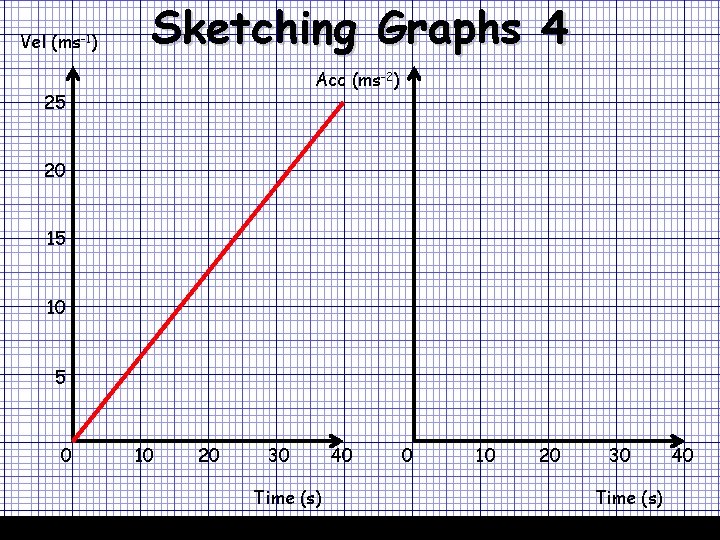
Vel (ms-1) Sketching Graphs 4 07/12/2020 Acc (ms-2) 25 20 15 10 5 0 10 20 30 Time (s) 40

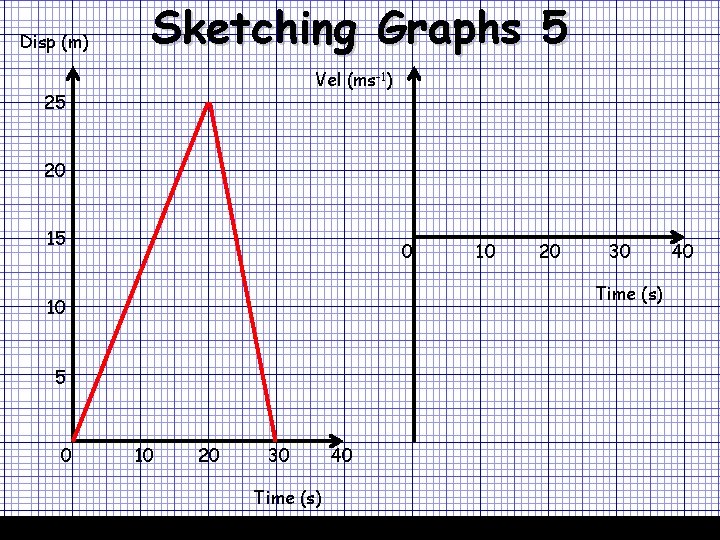
Disp (m) Sketching Graphs 5 07/12/2020 Vel (ms-1) 25 20 15 0 20 30 Time (s) 10 5 0 10 10 20 30 Time (s) 40 40

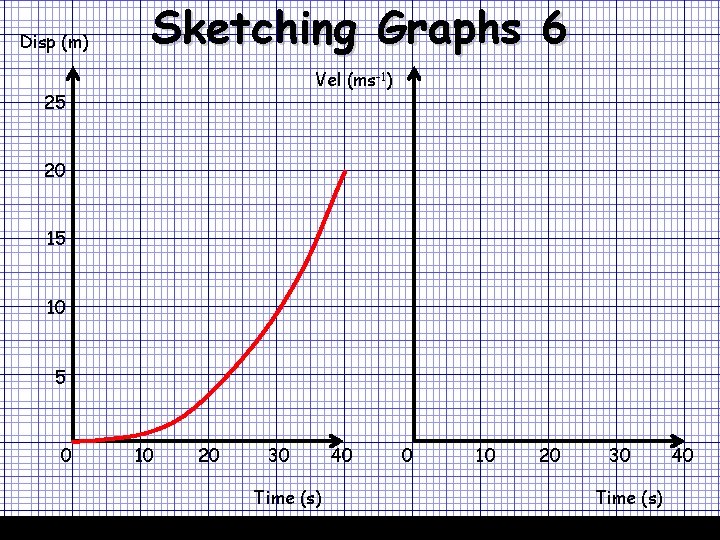
Disp (m) Sketching Graphs 6 07/12/2020 Vel (ms-1) 25 20 15 10 5 0 10 20 30 Time (s) 40

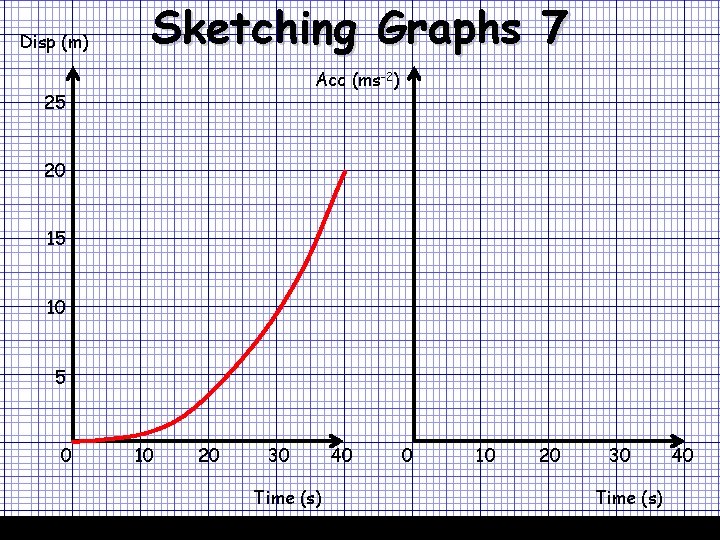
Disp (m) Sketching Graphs 7 07/12/2020 Acc (ms-2) 25 20 15 10 5 0 10 20 30 Time (s) 40

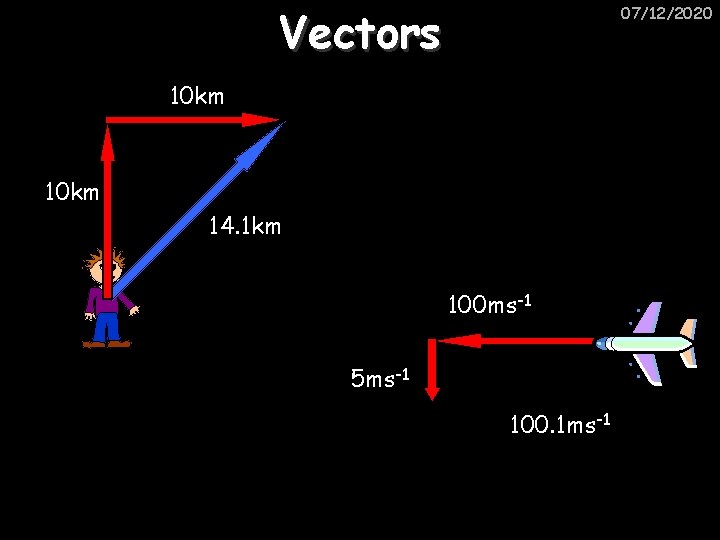
Vectors 07/12/2020 10 km 14. 1 km 100 ms-1 5 ms-1 100. 1 ms-1

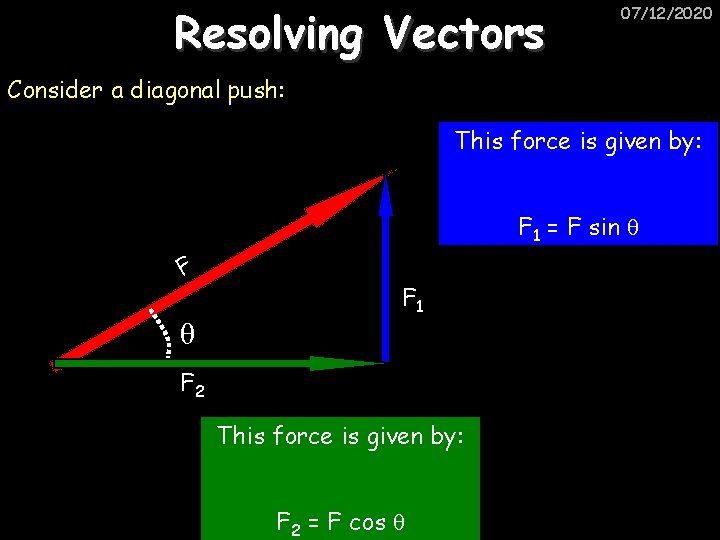
Resolving Vectors 07/12/2020 Consider a diagonal push: This force is given by: F 1 = F sin θ F 1 F 2 This force is given by: F 2 = F cos θ

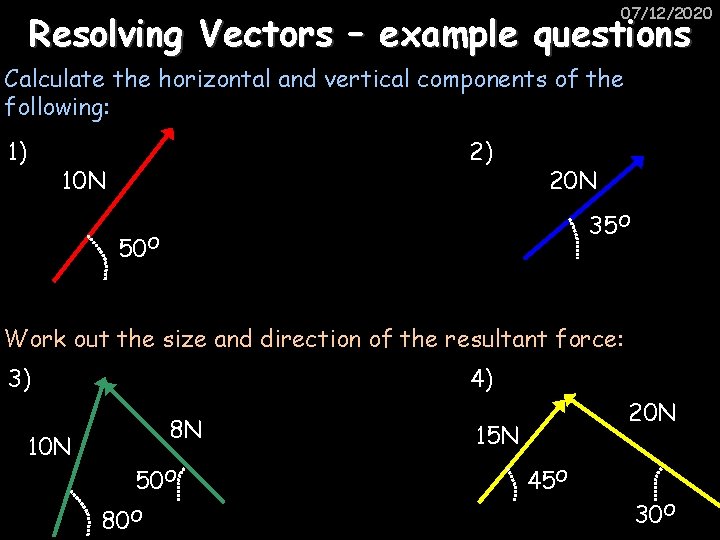
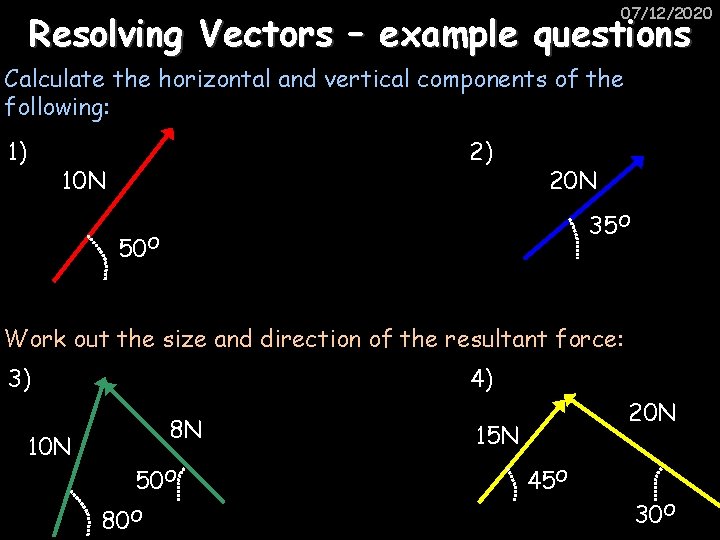
07/12/2020 Resolving Vectors – example questions Calculate the horizontal and vertical components of the following: 1) 2) 10 N 20 N 35 O 50 O Work out the size and direction of the resultant force: 3) 4) 8 N 10 N 50 O 80 O 20 N 15 N 45 O 30 O

More Questions 07/12/2020 1) Joe hikes 5 km north and then 9 km east. This journey takes him 2 hours. Draw, on graph paper, a scale diagram to show this movement and calculate: 1) The displacement at the end of the journey 2) His average speed 3) His average velocity 2) An aeroplane takes off with a velocity of 110 ms-1 at an angle of 25 O to the horizontal runway. Calculate the horizontal and vertical components of the plane’s velocity. 3) A coin is flicked off a table with a horizontal speed of 2 ms-1. Calculate its new speed 1 second later.

Drawing Vectors 07/12/2020

07/12/2020 A Practical Example of Resolving Vectors

Resolving Vectors Two blokes are holding a 10 kg wooden block like this: The block is stationary. If the angle between the rope and the horizontal is 100 calculate the tension in each rope. 07/12/2020

Vertical Projection 07/12/2020 If I throw this ball upwards with a speed of 40 ms-1 how high will it go? Use v 2 = u 2 + 2 as 0 = 402 + (2 x -9. 81 x s) 0 = 1600 – 19. 62 s 1600 = 19. 62 s s = 1600/19. 62 s = 81. 5 m

Practice Questions 07/12/2020 1) How far will a cricket ball go if it is thrown upwards with an initial velocity of 10 ms-1? 2) How far will a table tennis ball go if it is thrown upwards with an initial velocity of 5 ms-1? 3) A human cannonball is projected vertically upwards and she reaches a vertical height of 20 m before coming back down. How fast was she going when she left the cannon? 4) A test tube falls off the table. If the table is 1 m high how fast was the test tube going when it hit the floor?

Projectile Motion Aha! If I let go of the branch when he fires his gun I’ll be safe because the bullet will go above me… 07/12/2020

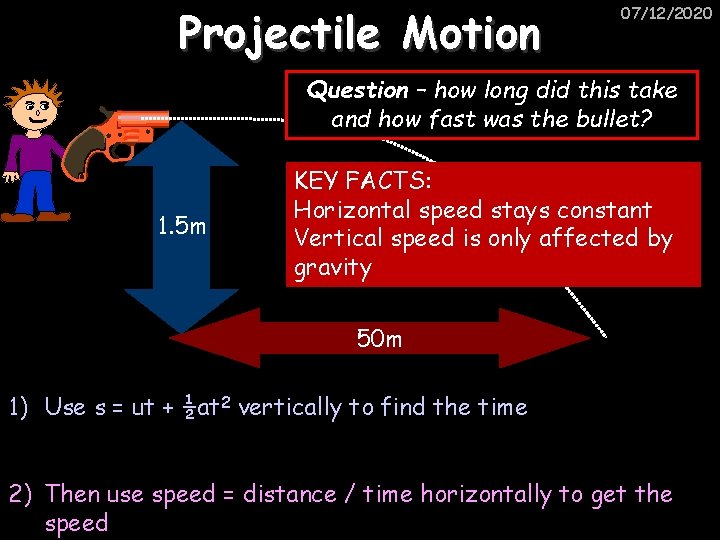
Projectile Motion 07/12/2020 Question – how long did this take and how fast was the bullet? 1. 5 m KEY FACTS: Horizontal speed stays constant Vertical speed is only affected by gravity 50 m 1) Use s = ut + ½at 2 vertically to find the time 2) Then use speed = distance / time horizontally to get the speed

Example questions 07/12/2020 1) Lauren throws a bowling ball at Tom and it lands on his foot. If the ball started 1. 2 m above Tom’s foot and the distance between them was 2 m calculate both the time taken and the initial velocity of the ball. 2) Sam fires a gun and the bullet leaves the barrel at a speed of 200 ms-1. If it landed on the ground 500 m away calculate how long the journey took and how high up Sam was holding the gun from ground level. 3) Fergus likes knocking test tubes off the table. If he hits one with an initial velocity of 2 ms-1 and the table is 1 m high calculate the time taken for the test tube to hit the floor and how far away from the table it landed.

Recap questions 07/12/2020 1) Andrew Murray hits a tennis ball and it passes horizontally over the net and lands just inside the baseline of the court. The net has a height of 1. 07 m and is 11. 9 m from the baseline. Find the horizontal speed of the ball. 2) Aguero takes a free kick and it flies into the top corner horizontally. If the corner is 2. 4 m above the ground and the goal is 18 m away calculate the time taken for the ball to reach the goal.

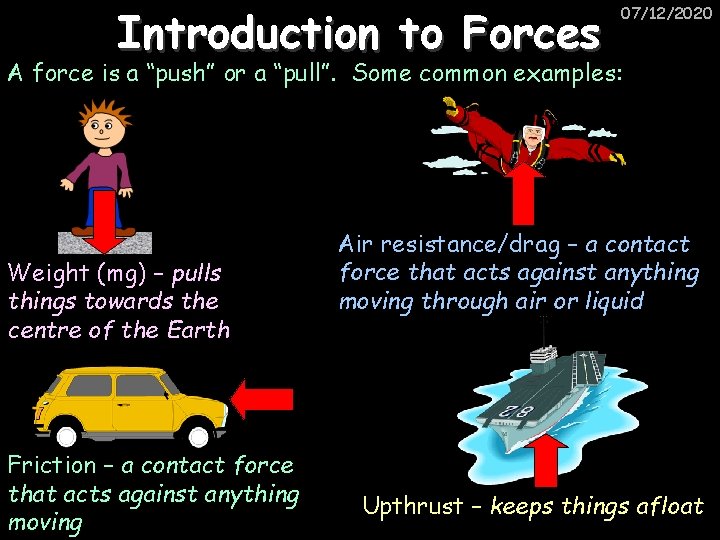
Introduction to Forces 07/12/2020 A force is a “push” or a “pull”. Some common examples: Weight (mg) – pulls things towards the centre of the Earth Friction – a contact force that acts against anything moving Air resistance/drag – a contact force that acts against anything moving through air or liquid Upthrust – keeps things afloat

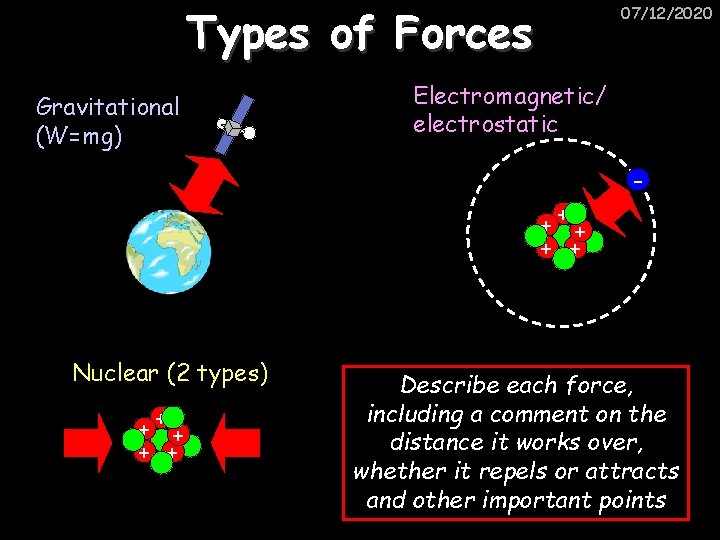
Types of Forces Gravitational (W=mg) 07/12/2020 Electromagnetic/ electrostatic +++ + + Nuclear (2 types) +++ + + Describe each force, including a comment on the distance it works over, whether it repels or attracts and other important points

Newton’s st 1 Law of Motion 07/12/2020 Basically, a body will remain at rest or continue to move with constant velocity as long as the forces acting on it are balanced (the sum of the vector forces is zero). …and an unbalanced Newton 1642 -1727 backwards force will make me slow down… An unbalanced forwards force will make me accelerate…

Newton’s nd 2 Law of Motion 07/12/2020 The acceleration of a body is proportional to the resultant force causing its acceleration and is in the same direction. Newton 1642 -1727 In other words… Resultant force = mass x acceleration ΣF = ma

Revision questions 1) A force of 1000 N is applied to push a mass of 500 kg. How quickly does it accelerate? F 2) A force of 3000 N acts on a car to make it accelerate by 1. 5 ms-2. How heavy is the car? 3) A car accelerates at a rate of 5 ms-2. If it weighs 500 kg how much driving force is the engine applying? 4) A force of 10 N is applied by a boy while lifting a 20 kg mass. How much does it accelerate by? 07/12/2020 M A

Slightly harder questions 07/12/2020 1) This car has a mass of 1000 kg. The engine exerts a driving force of 5, 000 N and a frictional force of 2, 000 N acts against it. What is its acceleration? 200 N 100 N 2) This body has a mass of 50 kg and is acted on by the forces shown. What will its acceleration be and at which angle (to the vertical)?

Resolving Force Vectors Another guy is dragging a 1. 5 kg box along the ground with a force of 20 N. The block is stuck in a groove and can’t move upwards. If the block accelerates from rest to 10 ms-1 in 5 s calculate: 1) The block’s acceleration 2) The size of the resultant force on the block 3) The size of the frictional force on the block 200 07/12/2020

Weight vs. Mass 07/12/2020 Earth’s Gravitational Field Strength is 10 Nkg-1. In other words, a 1 kg mass is pulled downwards by a force of 10 N. W Weight = Mass x Gravitational Field Strength (in N) (in kg) (in Nkg-1) M g 1) What is the weight on Earth of a book with mass 2 kg? 2) What is the weight on Earth of an apple with mass 100 g? 3) Matt weighs 700 N on the Earth. What is his mass? 4) On the moon the gravitational field strength is 1. 6 Nkg -1. What will Matt weigh if he stands on the moon?

Gravitational Fields 07/12/2020 Recall the equation: Weight = mass x gravitational field strength W = mg This equation related mass to weight. Mass is a scalar quantity but weight, being a force, is vector. Notice that g has two names and units: The gravitational field strength g = 9. 81 Nkg-1 The acceleration due to gravity g = 9. 81 ms-2

Terminal Velocity Consider a ball falling through a liquid: Some questions to consider: 1) What forces are acting on the ball? 2) How do those forces change when the ball gets faster? 3) Will the ball keep getting faster? Explain your answer in terms of forces 07/12/2020

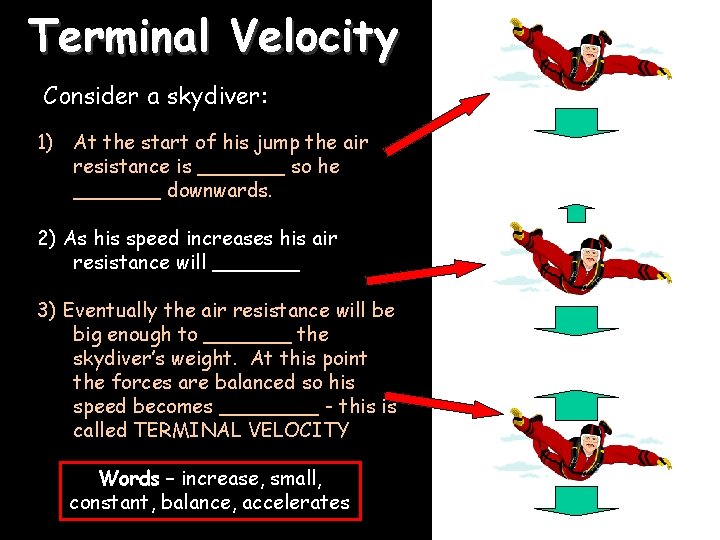
Terminal Velocity Consider a skydiver: 1) At the start of his jump the air resistance is _______ so he _______ downwards. 2) As his speed increases his air resistance will _______ 3) Eventually the air resistance will be big enough to _______ the skydiver’s weight. At this point the forces are balanced so his speed becomes ____ - this is called TERMINAL VELOCITY Words – increase, small, constant, balance, accelerates 07/12/2020

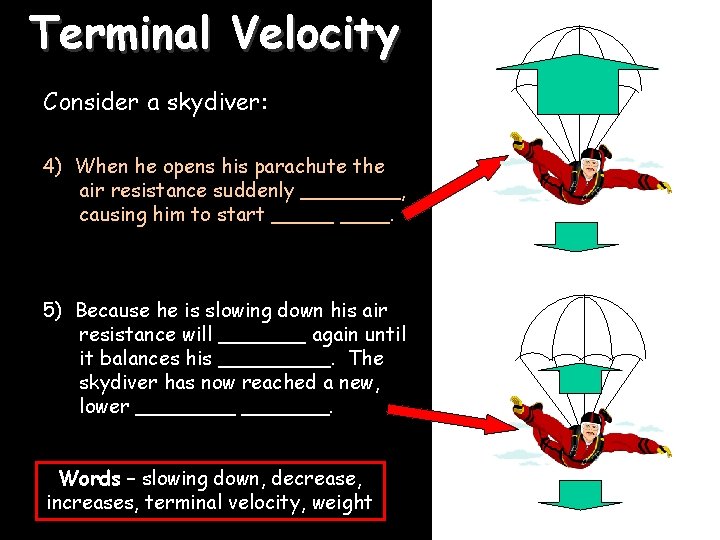
Terminal Velocity Consider a skydiver: 4) When he opens his parachute the air resistance suddenly ____, causing him to start _____. 5) Because he is slowing down his air resistance will _______ again until it balances his _____. The skydiver has now reached a new, lower _______. Words – slowing down, decrease, increases, terminal velocity, weight 07/12/2020

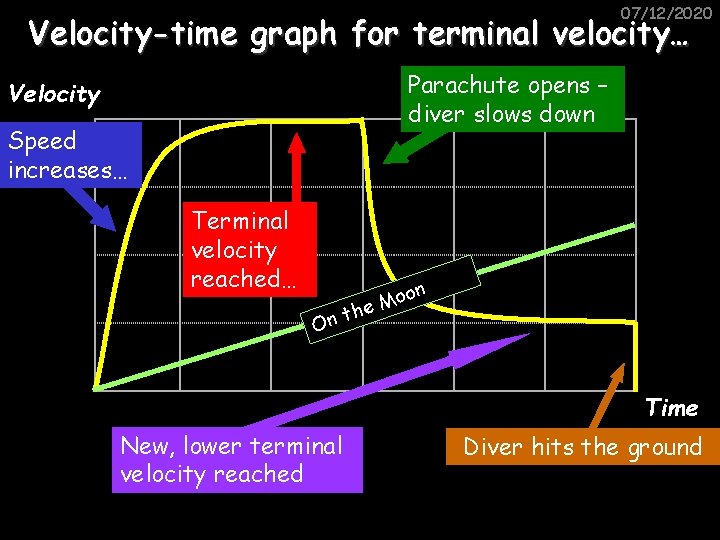
07/12/2020 Velocity-time graph for terminal velocity… Parachute opens – diver slows down Velocity Speed increases… Terminal velocity reached… On oon M he t Time New, lower terminal velocity reached Diver hits the ground

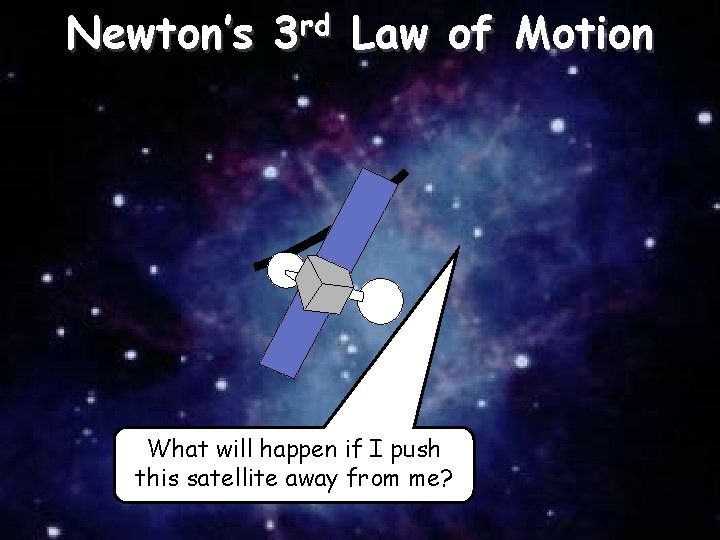
Newton’s rd 3 Law of Motion 07/12/2020 When body A exerts a force on body B, body B exerts an equal and opposite force on body A. My third law says that if I push to the right I will move backwards as well. Newton 1642 -1727

Newton’s rd 3 Law of Motion What will happen if I push this satellite away from me? 07/12/2020

Newton’s 3 Laws recap 07/12/2020 1) “If the forces acting on an object are balanced then that object is either stationary or moving with constant speed” 2) The resultant force is proportional to the object’s rate of change of momentum 3) Every force has an equal and opposite reaction

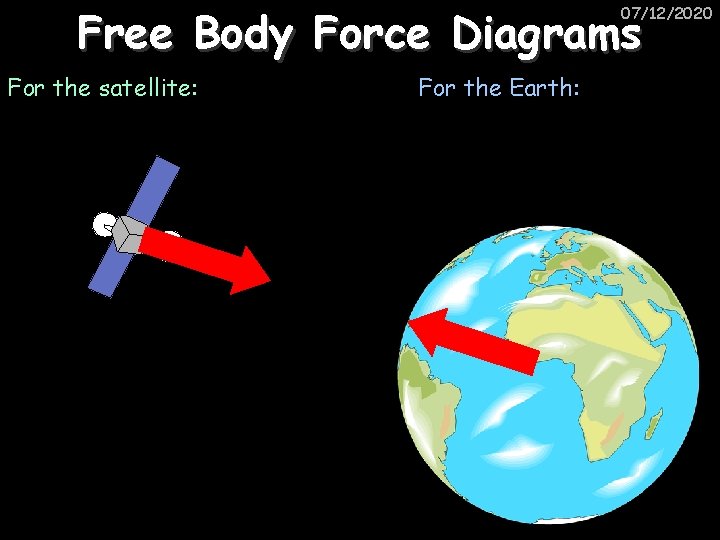
Free body force diagrams 07/12/2020 The Earth pulls Newton down with a gravitational force of 700 N. direction what type size Newton pulls the Earth up with a gravitational force of 700 N. This is a Newton III pair of forces

Free body force diagrams 2 07/12/2020 Consider a man standing on a table on the Earth:

Newton I vs. Newton III 07/12/2020 These two forces are acting on the same body, they’re two different types of force and the man is in equilibrium as long as the forces balance – this is a “Newton I pair of forces”. These two forces are acting on different bodies, they’re both the same type and they are always equal and opposite – this is a “Newton III pair of forces”.

Summary Newton I A law about the forces on _ ____ 07/12/2020 Newton III A law about the forces on _______ Concerns any _____ of forces Always concerns ____ forces only The forces can be ______ types Both forces are ______ type If there are two forces and the body is in equilibrium the forces are _____ The two forces are ALWAYS ______ Newton I only applies when the body is in ____ Newton III ______ applies

Free Body Force Diagrams 07/12/2020 For the satellite: For the Earth:

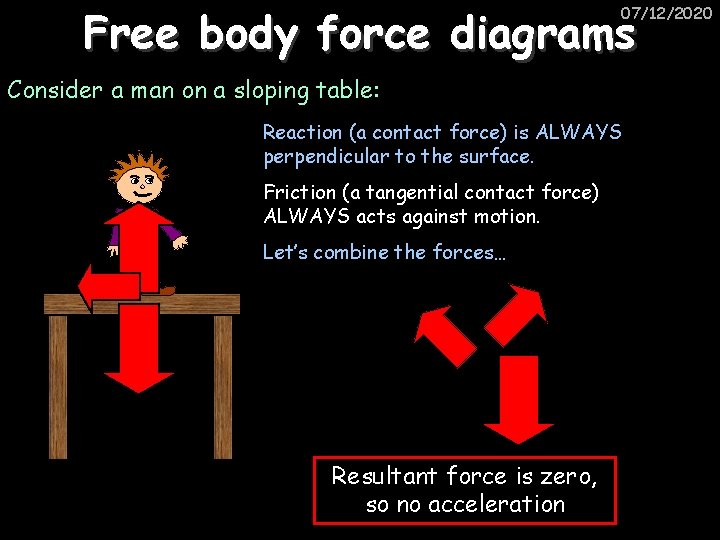
Free body force diagrams 07/12/2020 Consider a man on a sloping table: Reaction (a contact force) is ALWAYS perpendicular to the surface. Friction (a tangential contact force) ALWAYS acts against motion. Let’s combine the forces… Resultant force is zero, so no acceleration

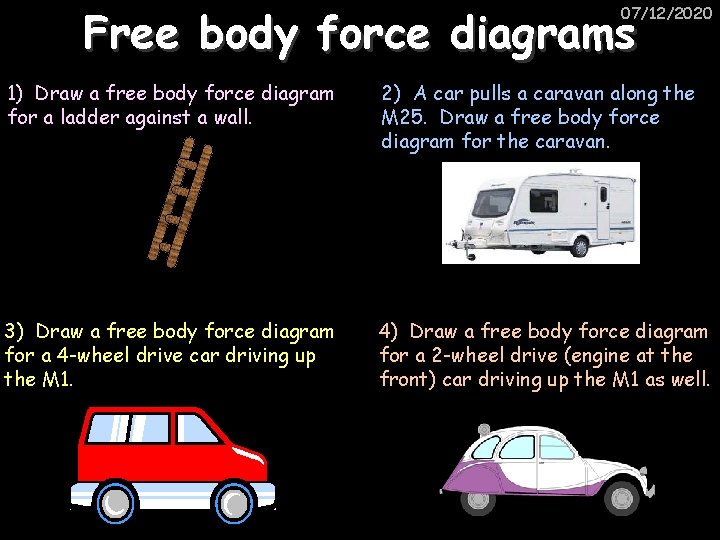
Free body force diagrams 07/12/2020 1) Draw a free body force diagram for a ladder against a wall. 2) A car pulls a caravan along the M 25. Draw a free body force diagram for the caravan. 3) Draw a free body force diagram for a 4 -wheel drive car driving up the M 1. 4) Draw a free body force diagram for a 2 -wheel drive (engine at the front) car driving up the M 1 as well.

07/12/2020

07/12/2020

07/12/2020

07/12/2020

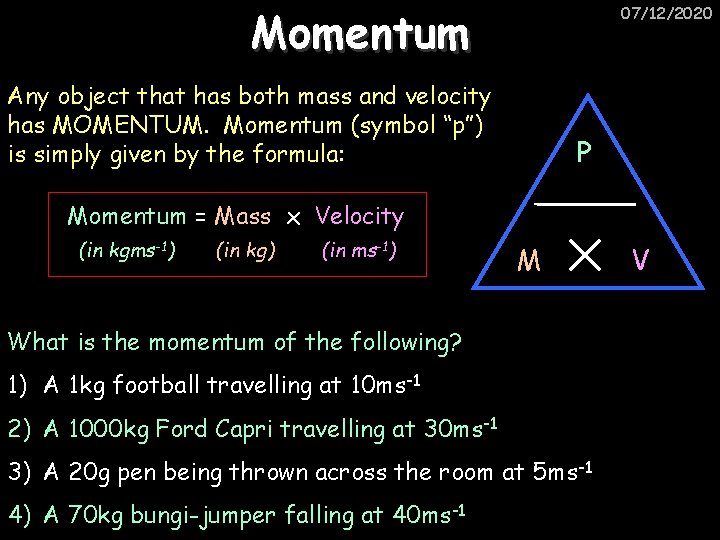
Momentum 07/12/2020 Any object that has both mass and velocity has MOMENTUM. Momentum (symbol “p”) is simply given by the formula: P Momentum = Mass x Velocity (in kgms-1) (in kg) (in ms-1) M What is the momentum of the following? 1) A 1 kg football travelling at 10 ms-1 2) A 1000 kg Ford Capri travelling at 30 ms-1 3) A 20 g pen being thrown across the room at 5 ms-1 4) A 70 kg bungi-jumper falling at 40 ms-1 V

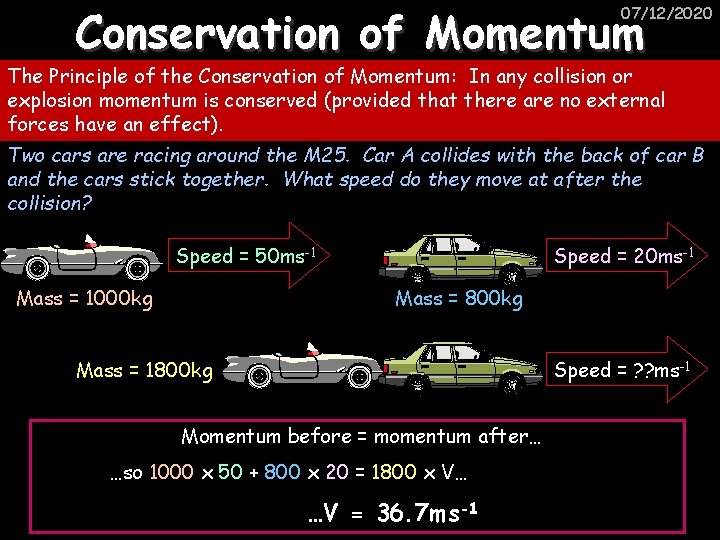
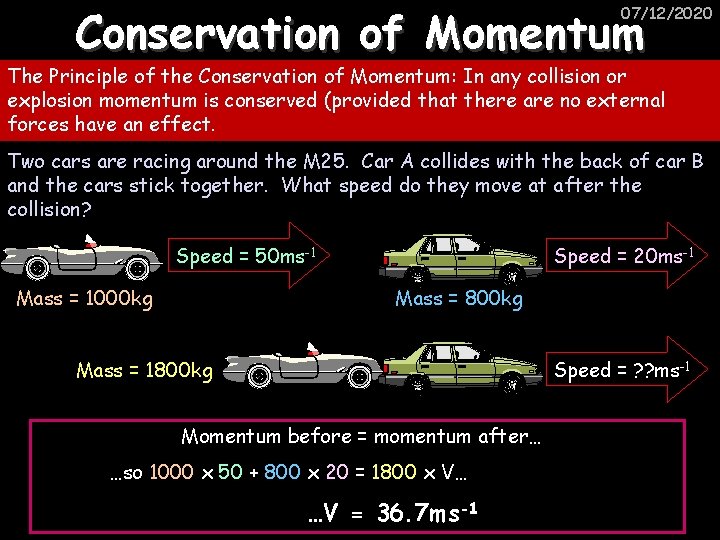
Conservation of Momentum 07/12/2020 The Principle of the Conservation of Momentum: In any collision or explosion momentum is conserved (provided that there are no external forces have an effect). Two cars are racing around the M 25. Car A collides with the back of car B and the cars stick together. What speed do they move at after the collision? Speed = 50 ms-1 Mass = 1000 kg Speed = 20 ms-1 Mass = 800 kg Mass = 1800 kg Speed = ? ? ms-1 Momentum before = momentum after… …so 1000 x 50 + 800 x 20 = 1800 x V… …V = 36. 7 ms-1

07/12/2020 Momentum in different directions What happens if the bodies are moving in opposite directions? Speed = 50 ms-1 Mass = 1000 kg Speed = 20 ms-1 Mass = 800 kg Momentum is a VECTOR quantity, so the momentum of the second car is negative… Total momentum = 1000 x 50 – 800 x 20 = 34000 kgms-1 Speed after collision = 34000 kgms-1 / 1800 = 18. 9 ms-1

Another example 07/12/2020 Consider the nuclear decay of Americium-241: 237 93 Np 241 95 Am If the new neptunium atom moves away at a speed of 5 x 105 ms-1 what was the speed of the alpha particle? 4 2 α

More questions… 07/12/2020 1) A white snooker ball moving at 5 ms-1 strikes a red ball and pots it. Both balls have a mass of 1 kg. If the white ball continued in the same direction at 2 ms-1 what was the velocity of the red ball? 2) A car of mass 1000 kg heading up the M 1 at 50 ms-1 collides with a stationary truck of mass 8000 kg and sticks to it. What velocity does the wreckage move forward at? 3) A defender running away from a goalkeeper at 5 ms-1 is hit in the back of his head by the goal kick. The ball stops dead and the player’s speed increases to 5. 5 ms-1. If the ball had a mass of 500 g and the player had a mass of 70 kg how fast was the ball moving? 4) A gun has a recoil speed of 2 ms-1 when firing. If the gun has a mass of 2 kg and the bullet has a mass of 10 g what speed does the bullet come out at?

Newton’s nd 2 Law and Impulse 07/12/2020 Instead of F=ma Newton actually said that the force acting on an object is that object’s rate of change of momentum. In other words… mv Force = Change in momentum (in kgms-1) (in N) Time (in s) Also called “impulse” F T For example, Wayne Rooney takes a free kick by kicking a stationary football with a force of 40 N. If the ball has a mass of 0. 5 kg and his foot is in contact with the ball for 0. 1 s calculate: 1) The change in momentum of the ball (its impulse), 2) The speed the ball moves away with

Example questions 07/12/2020 1) Alice likes playing golf. She strikes a golf ball with a force of 80 N. If the ball has a mass of 200 g and the club is in contact with it for 0. 2 s calculate a) the change in momentum of the golf ball, b) its speed. 2) Sam thinks it’s funny to hit tennis balls at Sean. He strikes a serve with a force of 30 N. If the ball has a mass of 250 g and the racket is in contact with it for 0. 15 s calculate the ball’s change in momentum and its speed. 3) Dom takes a dropkick by kicking a 0. 4 kg rugby ball away at 10 m/s. If his foot was in contact with the ball for 0. 1 seconds calculate the force he applied to the ball. 4) Steve strikes a 200 g golf ball away at 50 ms-1. If he applied a force of 50 N calculate how long his club was in contact with the ball for.

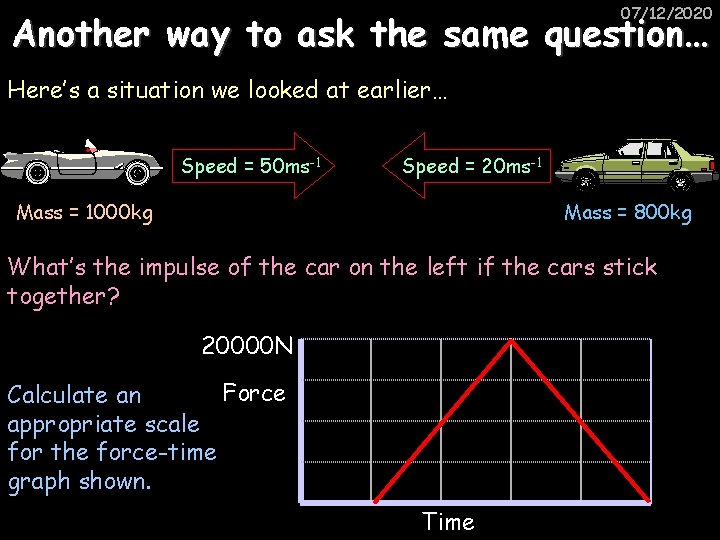
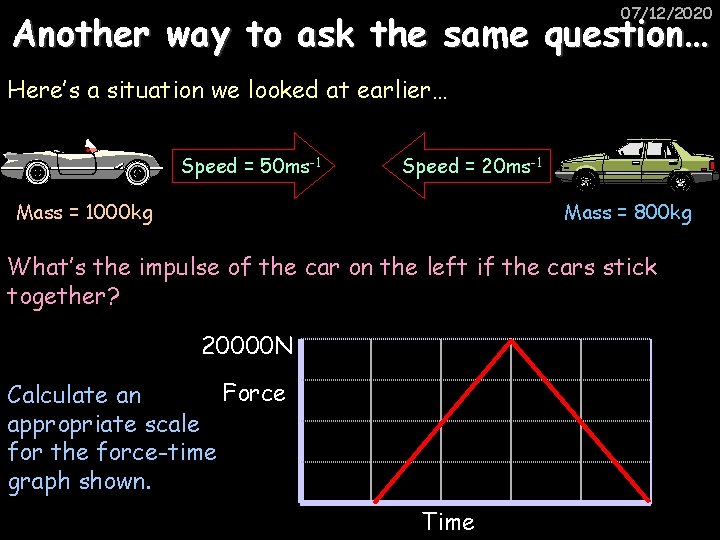
07/12/2020 Another way to ask the same question… Here’s a situation we looked at earlier… Speed = 50 ms-1 Speed = 20 ms-1 Mass = 1000 kg Mass = 800 kg What’s the impulse of the car on the left if the cars stick together? 20000 N Force Calculate an appropriate scale for the force-time graph shown. Time

Momentum 07/12/2020 Any object that has both mass and velocity has MOMENTUM. Momentum (symbol “p”) is simply given by the formula: P Momentum = Mass x Velocity (in kgms-1) (in kg) (in ms-1) M What is the momentum of the following? 1) A 1 kg football travelling at 10 ms-1 2) A 1000 kg Ford Capri travelling at 30 ms-1 3) A 20 g pen being thrown across the room at 5 ms-1 4) A 70 kg bungi-jumper falling at 40 ms-1 V

Newton’s nd 2 Law and Impulse 07/12/2020 Instead of F=ma Newton actually said that the force acting on an object is that object’s rate of change of momentum. In other words… p Force = Change in momentum (in kgms-1) (in N) Time (in s) Also called “impulse” F T For example, Sturridge scores from a free kick by kicking a stationary football with a force of 40 N. If the ball has a mass of 0. 5 kg and his foot is in contact with the ball for 0. 1 s calculate: 1) The change in momentum of the ball (its impulse), 2) The speed the ball moves away with

Example questions 07/12/2020 1) Jack likes playing golf. He strikes a golf ball with a force of 80 N. If the ball has a mass of 200 g and the club is in contact with it for 0. 2 s calculate a) the change in momentum of the golf ball, b) its speed. 2) Chad thinks it’s funny to hit tennis balls at Sam. He strikes a serve with a force of 30 N. If the ball has a mass of 250 g and the racket is in contact with it for 0. 15 s calculate the ball’s change in momentum and its speed. 3) Olly takes a dropkick by kicking a 0. 4 kg rugby ball away at 10 m/s. If his foot was in contact with the ball for 0. 1 seconds calculate the force he applied to the ball. 4) Paddy strikes a 200 g golf ball away at 50 m/s. If he applied a force of 50 N calculate how long his club was in contact with the ball for.

07/12/2020 Another way to ask the same question… Here’s a situation we looked at earlier… Speed = 50 ms-1 Speed = 20 ms-1 Mass = 1000 kg Mass = 800 kg What’s the impulse of the car on the left if the cars stick together? 20000 N Force Calculate an appropriate scale for the force-time graph shown. Time

Conservation of Momentum 07/12/2020 The Principle of the Conservation of Momentum: In any collision or explosion momentum is conserved (provided that there are no external forces have an effect. Two cars are racing around the M 25. Car A collides with the back of car B and the cars stick together. What speed do they move at after the collision? Speed = 50 ms-1 Mass = 1000 kg Speed = 20 ms-1 Mass = 800 kg Mass = 1800 kg Speed = ? ? ms-1 Momentum before = momentum after… …so 1000 x 50 + 800 x 20 = 1800 x V… …V = 36. 7 ms-1

07/12/2020 Momentum in different directions What happens if the bodies are moving in opposite directions? Speed = 50 ms-1 Mass = 1000 kg Speed = 20 ms-1 Mass = 800 kg Momentum is a VECTOR quantity, so the momentum of the second car is negative… Total momentum = 1000 x 50 – 800 x 20 = 34000 kgms-1 Speed after collision = 34000 kgms-1 / 1800 = 18. 9 ms-1

Another example 07/12/2020 Consider the nuclear decay of Americium-241: 237 93 Np 241 95 Am If the new neptunium atom moves away at a speed of 5 x 105 ms-1 what was the speed of the alpha particle? 4 2 α

More questions… 07/12/2020 1) A white snooker ball moving at 5 ms-1 strikes a red ball and pots it. Both balls have a mass of 1 kg. If the white ball continued in the same direction at 2 ms-1 what was the velocity of the red ball? 2) A car of mass 1000 kg heading up the M 1 at 50 ms-1 collides with a stationary truck of mass 8000 kg and sticks to it. What velocity does the wreckage move forward at? 3) A defender running away from a goalkeeper at 5 ms-1 is hit in the back of his head by the goal kick. The ball stops dead and the player’s speed increases to 5. 5 ms-1. If the ball had a mass of 500 g and the player had a mass of 70 kg how fast was the ball moving? 4) A gun has a recoil speed of 2 ms-1 when firing. If the gun has a mass of 2 kg and the bullet has a mass of 10 g what speed does the bullet come out at?

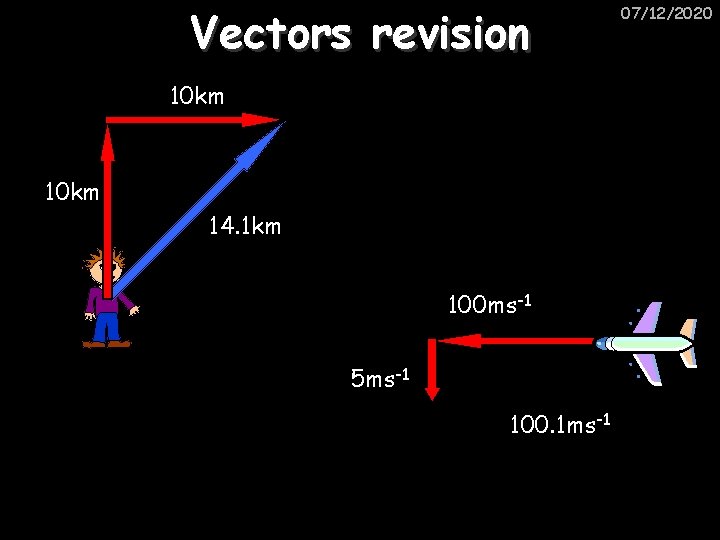
Vectors revision 10 km 14. 1 km 100 ms-1 5 ms-1 100. 1 ms-1 07/12/2020

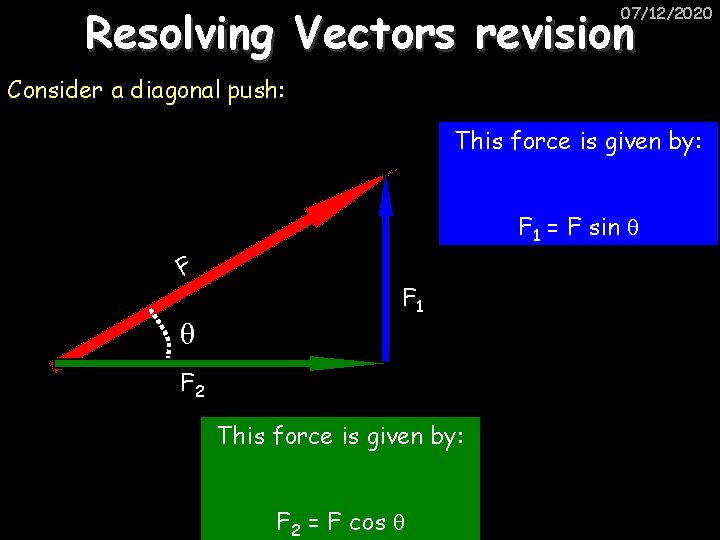
Resolving Vectors revision 07/12/2020 Consider a diagonal push: This force is given by: F 1 = F sin θ F 1 F 2 This force is given by: F 2 = F cos θ

07/12/2020 Resolving Vectors – example questions Calculate the horizontal and vertical components of the following: 1) 2) 10 N 20 N 35 O 50 O Work out the size and direction of the resultant force: 3) 4) 8 N 10 N 50 O 80 O 20 N 15 N 45 O 30 O

07/12/2020 Linear Momentum in two dimensions A practical example:

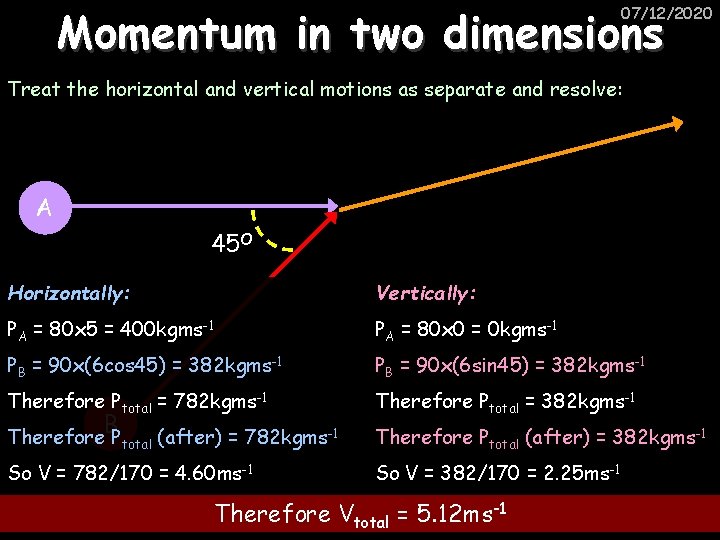
07/12/2020 Linear Momentum in two dimensions Imagine a rugby tackle: Q. The first player (and the ball) have a combined mass of 80 kg and a speed of 5 ms-1. The second player has a mass of 90 kg and tackles him at an angle of 45 O and a speed of 6 ms-1. If the players stick together what is their new speed after the tackle?

Momentum in two dimensions 07/12/2020 Treat the horizontal and vertical motions as separate and resolve: A 45 O Horizontally: Vertically: PA = 80 x 5 = 400 kgms-1 PA = 80 x 0 = 0 kgms-1 PB = 90 x(6 cos 45) = 382 kgms-1 PB = 90 x(6 sin 45) = 382 kgms-1 Therefore Ptotal = 782 kgms-1 Therefore Ptotal = 382 kgms-1 Therefore Ptotal (after) = 782 kgms-1 Therefore Ptotal (after) = 382 kgms-1 So V = 782/170 = 4. 60 ms-1 So V = 382/170 = 2. 25 ms-1 B Therefore Vtotal = 5. 12 ms-1

Momentum in two dimensions 07/12/2020 Kien is playing pool. He hits the white ball and it travels with a speed of 4 ms-1. The white ball has a mass of 0. 17 kg and it strikes the black ball, causing the black ball to move away at an angle of 30 O. What speed does each ball move away with? 30 O

Test 07/12/2020 1) A movie stuntman with a mass of 100 kg stands on a stationary 1 kg skateboard. He gets shot by a 9 mm pistol firing an 8 g bullet. The bullet leaves the gun at 370 ms -1 and embeds in the vest. How fast will the stuntman move away? 2) In another movie scene a stuntman with a mass of 80 kg leaps from a train onto a 120 kg boat. His speed was 12 ms -1 and he landed on the boat at an angle of 20 O to the direction of the current (which the boat will move in after he lands). How fast will the boat and man move off down the river?

Another example of an explosion 07/12/2020 50 Kg, moving at an angle of 70 O to the vertical Missing velocities? 10 Kg, moving with a velocity of 20 ms-1 at an angle of 80 O to the vertical 20 Kg, moving at an angle of 120 O to the vertical

Energy loss in collisions 07/12/2020 Recall our equation for kinetic energy: Kinetic energy = ½ x mass x velocity squared We’ve also said that in a collision momentum is conserved (unless an external force acts). The same cannot usually be said for kinetic energy… For example, consider the following collision. How much kinetic energy is lost? Before Speed = 50 ms-1 Speed = 20 ms-1 Mass = 1000 kg Mass = 800 kg After Mass = 1000 kg Speed = 20 ms-1 Mass = 800 kg Speed = 30 ms-1

Energy loss in collisions 07/12/2020 Consider a head-on collision where the cars stick together. How much kinetic energy is lost in this example? Where does all the energy go? Before Speed = 50 ms-1 m=800 Kg Speed = 30 ms-1 m=3000 Kg After Speed = 10 ms-1 In this example more kinetic energy was lost. We say it was a “less elastic collision”. An “elastic collision” is one where the kinetic energy is conserved.

Particle energy 07/12/2020 When dealing with objects as small as particles it’s useful to derive another equation by combining equations we know for momentum and kinetic energy: Ek = ½ mv 2 p = mv By combining these equations we can say: Kinetic energy Ek = p 2 2 m

Example Questions 07/12/2020 Use mass of proton = 1. 67 x 10 -27 kg, mass of electron = 9. 11 x 10 -31 kg and e = 1. 6 x 10 -19 C 1) A positron has a momentum of 10 -25 kgms-1. Calculate its kinetic energy 2) Calculate the kinetic energy of an alpha particle of momentum 9 x 10 -20 kgms-1… a) In Joules b) In electronvolts

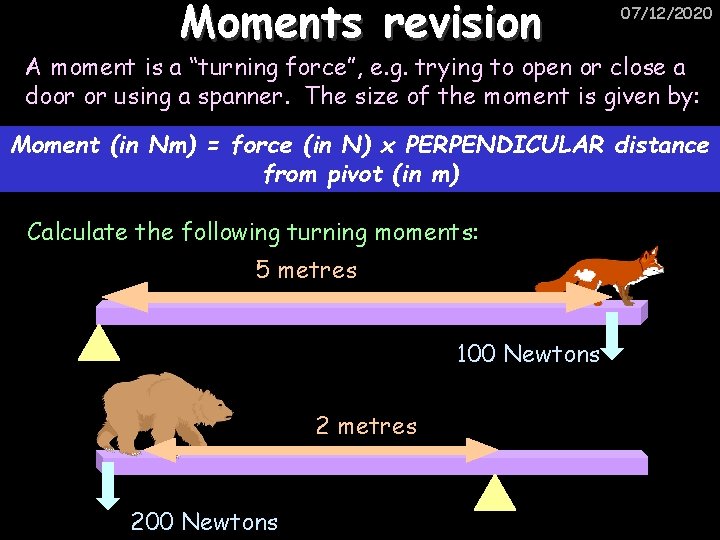
Moments revision 07/12/2020 A moment is a “turning force”, e. g. trying to open or close a door or using a spanner. The size of the moment is given by: Moment (in Nm) = force (in N) x PERPENDICULAR distance from pivot (in m) Calculate the following turning moments: 5 metres 100 Newtons 2 metres 200 Newtons

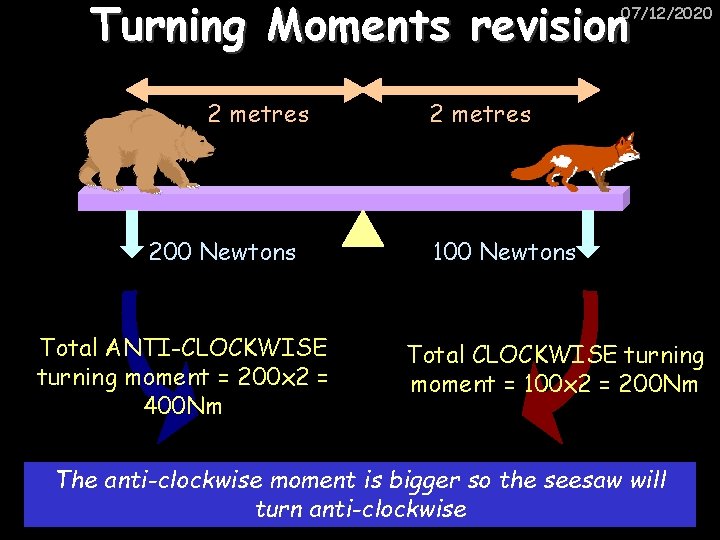
Turning Moments revision 07/12/2020 2 metres 200 Newtons Total ANTI-CLOCKWISE turning moment = 200 x 2 = 400 Nm 2 metres 100 Newtons Total CLOCKWISE turning moment = 100 x 2 = 200 Nm The anti-clockwise moment is bigger so the seesaw will turn anti-clockwise

Balanced or unbalanced? 07/12/2020

The Principle of Moments 07/12/2020 “If a body is in equilibrium the sum of the clockwise moments is equal to the sum of the anti-clockwise moments. ”

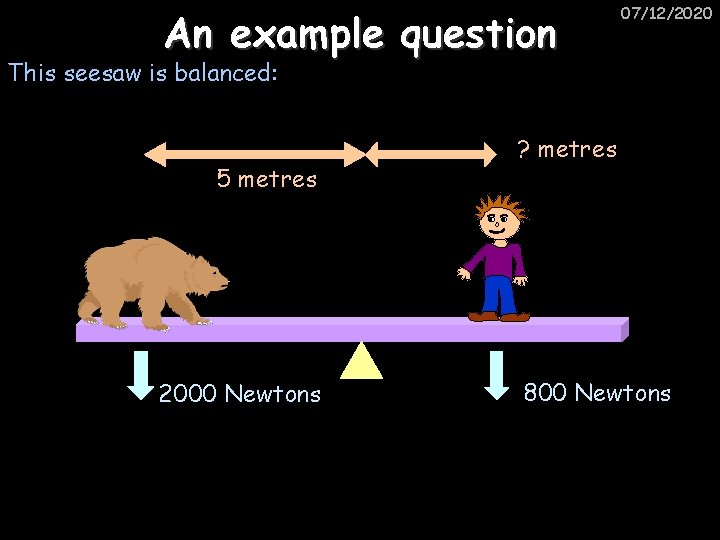
An example question 07/12/2020 This seesaw is balanced: 5 metres 2000 Newtons ? metres 800 Newtons

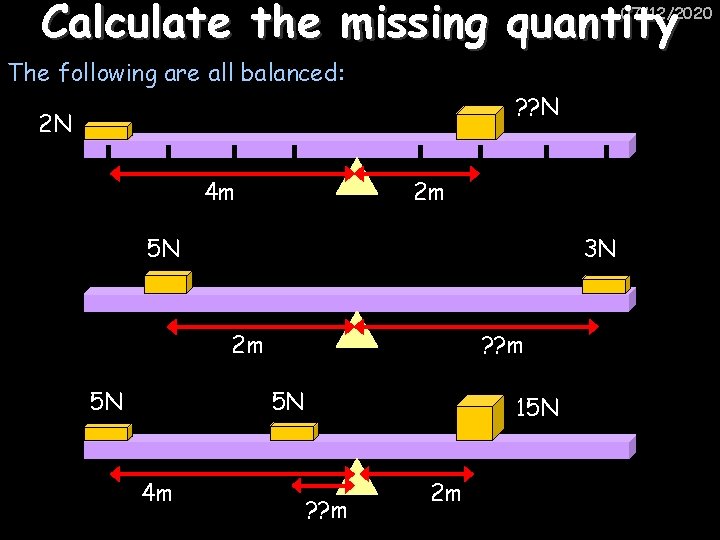
Calculate the missing quantity 07/12/2020 The following are all balanced: ? ? N 2 N 4 m 2 m 5 N 3 N 2 m 5 N ? ? m 5 N 4 m 15 N ? ? m 2 m

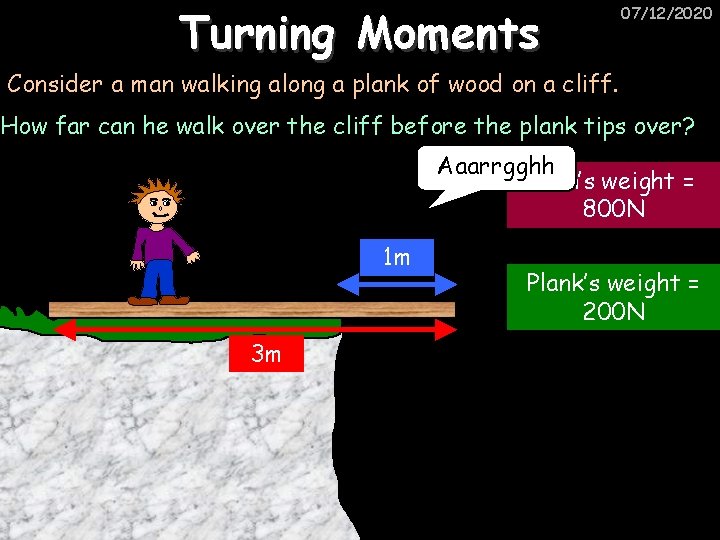
Turning Moments 07/12/2020 Consider a man walking along a plank of wood on a cliff. How far can he walk over the cliff before the plank tips over? Aaarrgghh Man’s weight = 800 N 1 m 3 m Plank’s weight = 200 N

A recap question 07/12/2020 1) State the principle of moments 2) Calculate the mass of man in the example given below: 30 kg 0. 4 m 1. 2 m

Types of Energy Recap Type Heat Kinetic (movement) Nuclear Sound Light Chemical Electrical Gravitational potential Elastic potential 07/12/2020 Something you know about it

Kinetic energy 07/12/2020 Any object that moves will have kinetic energy. The amount of kinetic energy an object has can be found using the formula: Kinetic energy = ½ x mass x velocity squared in J in kg Ek = ½ in m/s mv 2

Example questions 07/12/2020 1) Katie drives her car at a speed of 30 ms-1. If the combined mass of her and the car is 1000 kg what is her kinetic energy? 2) Ben rides his bike at a speed of 10 ms-1. If the combined mass of Ben and his bike is 80 kg what is his kinetic energy? 3) Will is running and has a kinetic energy of 750 J. If his mass is 60 kg how fast is he running? 4) Connor is walking to town. If he has a kinetic energy of 150 J and he’s walking at a pace of 2 ms-1 what is his mass?

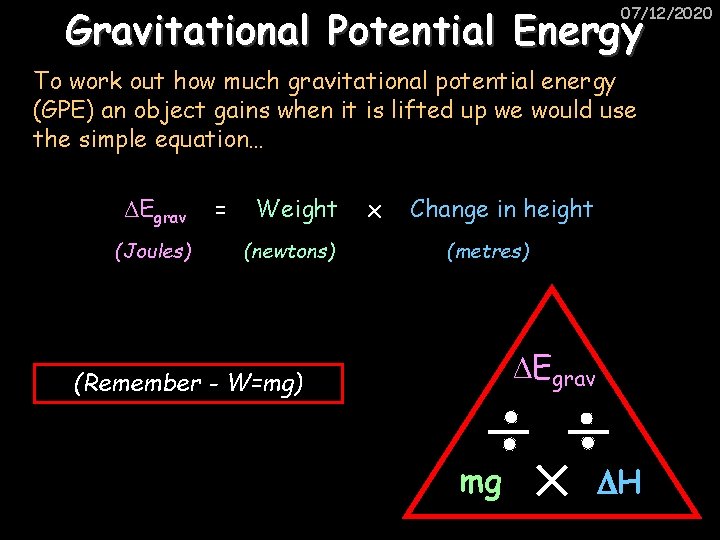
Gravitational Potential Energy 07/12/2020 To work out how much gravitational potential energy (GPE) an object gains when it is lifted up we would use the simple equation… ΔEgrav (Joules) = Weight (newtons) x Change in height (metres) ΔEgrav (Remember - W=mg) mg H

Some example questions… 07/12/2020 How much gravitational potential energy have the following objects gained? : 1. A brick that weighs 10 N lifted to the top of a house (10 m), 2. A 1, 000 kg car lifted by a ramp up to a height of 2 m, 3. A 70 kg person lifted up 50 cm by a friend. How much GPE have the following objects lost? : 1. A 2 N football dropping out of the air after being kicked up 30 m, 2. A 0. 5 N egg falling 10 m out of a bird nest, 3. A 1, 000 kg car falling off its 200 cm ramp.

Energy changes for a skydiver Recall our skydiver: If the skydiver has reached terminal velocity explain what happened to his… 1) Kinetic energy 2) Gravitational potential energy …during his skydive.

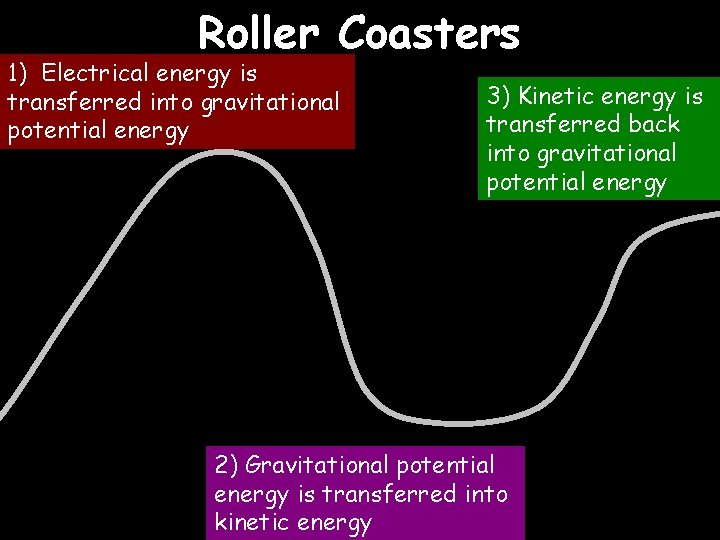
Roller Coasters 1) Electrical energy is transferred into gravitational potential energy 3) Kinetic energy is transferred back into gravitational potential energy 2) Gravitational potential energy is transferred into kinetic energy

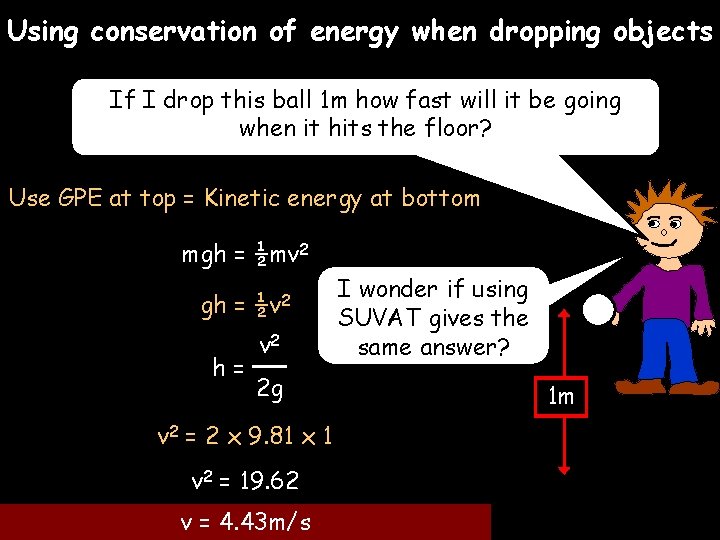
Using conservation of energy when dropping objects If I drop this ball 1 m how fast will it be going when it hits the floor? Use GPE at top = Kinetic energy at bottom mgh = ½mv 2 gh = h= ½v 2 2 g v 2 = 2 x 9. 81 x 1 v 2 = 19. 62 v = 4. 43 m/s I wonder if using SUVAT gives the same answer? 1 m

An example question… 07/12/2020 If the height of the drop was 100 m and assuming there was a 100% conversion from gravitational to kinetic energy, how fast was the roller coaster car moving at the bottom of the ramp?

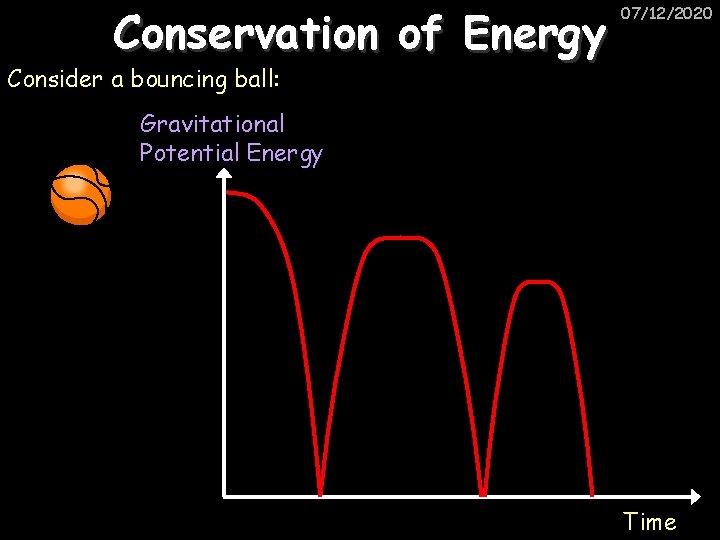
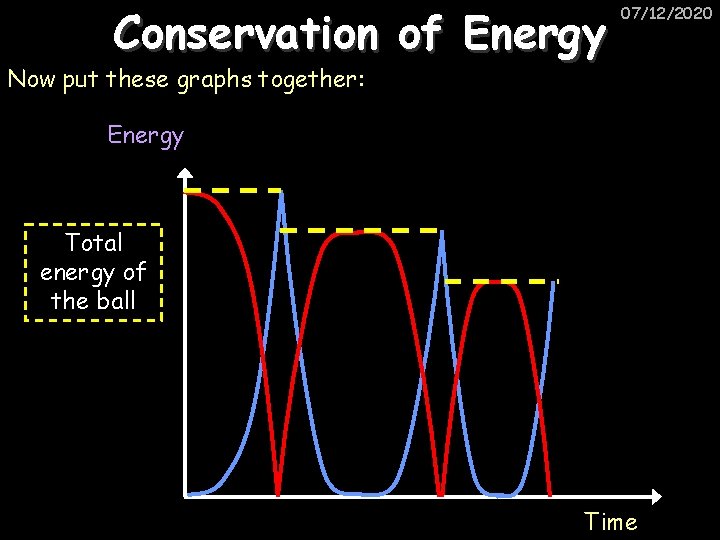
Conservation of Energy 07/12/2020 Consider a bouncing ball: Gravitational Potential Energy Time

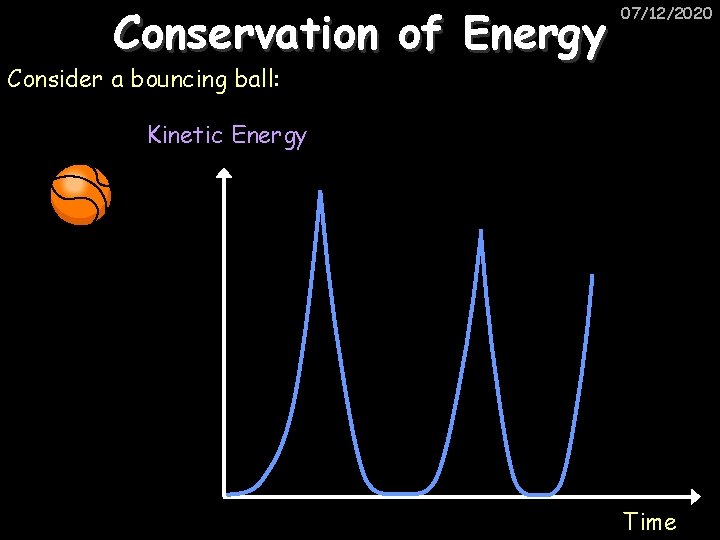
Conservation of Energy 07/12/2020 Consider a bouncing ball: Kinetic Energy Time

Conservation of Energy 07/12/2020 Now put these graphs together: Energy Total energy of the ball Time

Work done 07/12/2020 Work done (in joules) is simply the force needed to move an object multiplied by the distance moved in the direction of the force: ΔW ΔW = FΔs F Δs

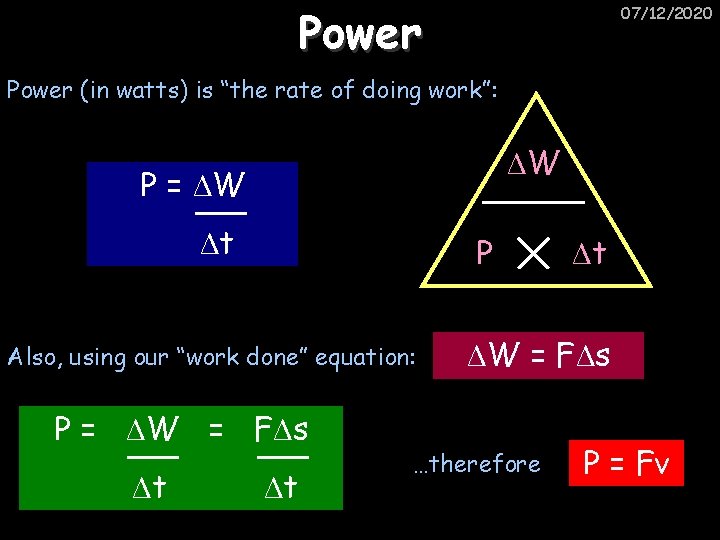
Power 07/12/2020 Power (in watts) is “the rate of doing work”: ΔW P = ΔW Δt P Also, using our “work done” equation: P = ΔW = FΔs Δt Δt Δt ΔW = FΔs …therefore P = Fv

Random questions on work and power 07/12/2020 1) Adam pushes Dan in the direction of a cliff. If he uses a force of 40 N and he moves Dan 10 m in 4 s calculate the work done and Adam’s power rating. 2) Richard runs up some stairs and has a power rating of 600 W while he does so. If he does it in 5 seconds and his weight is 750 N calculate how high the stairs are. 3) A man pulls a block of wood at an angle of 200 to the horizontal and uses a force of 50 N. If the distance travelled horizontally is 5 m calculate the work done by the man and his power if the journey lasted 10 seconds. 200 50 N

Efficiency revision 07/12/2020 Efficiency is a measure of how much USEFUL energy you get out of an object from the energy you put INTO it. For example, consider a TV: ) J 0 8 ( ight L Electrical Energy (200 J) Sound (40 J) Heat (? ) Efficiency = Useful energy out Energy in x 100%

Some examples of efficiency… 07/12/2020 1) 5000 J of electrical energy are put into a motor. The motor converts this into 100 J of movement energy. How efficient is it? 2) A laptop can convert 400 W of electrical power into 240 W of light and sound power. What is its efficiency? Where does the rest of the energy go? 3) A steam engine is 50% efficient. If it delivers 20, 000 W of movement power how much chemical energy was put into it every second?

07/12/2020 Materials

Density = Mass Volume 07/12/2020 ρ= m V 1) What is the density of a piece of wood of volume 2 m 3 and mass 1200 kg? 2) Air only has a density of 1. 3 kgm-3. What is the mass of 0. 2 m 3 of air? 3) Carbon dioxide is more dense and the same volume would have a mass of 0. 38 kg. What is its density? 4) The mercury in a thermometer has a volume of 5 x 10 -5 m 3. If the density of the mercury is 13600 kgm-3 what mass of mercury is in thermometer?

Floating recap 07/12/2020 Whether or not an object will float depends on its DENSITY. For example: The metal block will ____ because it is ______ dense than water The wooden block will ____ because it is ______ dense than water

Upthrust in Fluids 07/12/2020 Any object that is placed in a liquid will experience a force called upthrust. We can use my principle to calculate how big that upthrust is: Archimedes, 287 -212 BC Upthrust = weight of fluid displaced Weight Upthrust

Example questions 07/12/2020 A block of copper is suspended from a Newton meter. It is then submerged in water. The block is a cube of sides 30 cm. If copper has a density of 8960 kgm-3 calculate: 1) The block’s volume 2) The block’s mass 3) The block’s weight (what the Newton meter reads before submerging) 4) The weight of the water the block displaces (i. e. the upthrust) 5) The reading on the Newton meter when the block is submerged.

Recap question This block of granite is a cube of sides 3 cm and density 2750 kgm-3. The cube is suspended from a Newton meter and placed in water. What will the reading on the Newton meter be? 07/12/2020

Another recap question This block of marble is a cube of density 2500 kgm-3. The cube is suspended from a Newton meter and placed in water. The reading on the Newton meter decreased by 0. 08 N. What is the size of the cube? 07/12/2020

Testing aerodynamics 07/12/2020

Laminar Flow vs Turbulent Flow 07/12/2020 Laminar flow (seen here) is when “adjacent layers of a fluid do not cross over each other”.

Laminar Flow vs Turbulent Flow 07/12/2020

Terminal Velocity in a liquid 07/12/2020 Consider a ball falling through a liquid: Some questions to consider: 1) What forces are acting on the ball? 2) How do those forces change when the ball gets faster? 3) Will the ball keep getting faster? Explain your answer in terms of forces

Stokes’ Law 07/12/2020 When a sphere moves through a liquid the movement of the liquid relative to the sphere is laminar. It’s as though the particles of the fluid that are next to the sphere “stick” to it and move along with it. That’s quite interesting, but it would be even better if it was mathematical… Consider a sphere of radius r moving with a velocity v relative to a fluid with viscosity η: George Stokes, 1819 -1903 Viscous drag F = 6πηrv This is called Stokes’ Law, after me. It ONLY works for spheres moving at low speeds (i. e. laminar flow) Viscous drag

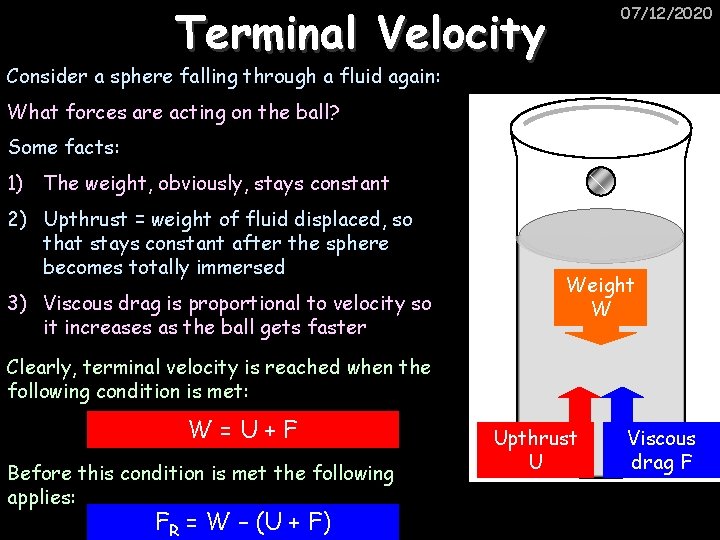
Terminal Velocity 07/12/2020 Consider a sphere falling through a fluid again: What forces are acting on the ball? Some facts: 1) The weight, obviously, stays constant 2) Upthrust = weight of fluid displaced, so that stays constant after the sphere becomes totally immersed 3) Viscous drag is proportional to velocity so it increases as the ball gets faster Weight W Clearly, terminal velocity is reached when the following condition is met: W=U+F Before this condition is met the following applies: FR = W – (U + F) Upthrust U Viscous drag F

Free body force diagrams 07/12/2020 Draw free body force diagrams and write a force equation for the following objects: 1) A ball bearing with a density just less than water floating on its surface: 2) A more dense ball bearing accelerating through a liquid: 3) The same ball bearing later when it has reached terminal velocity:

Free body force diagrams 07/12/2020 Draw free body force diagrams and write a force equation for the following objects: 1) A ball bearing with low density that’s accelerating towards the surface: 2) The same ball bearing when it has reached terminal velocity while rising: 3) The same ball bearing later when it has reached the surface:

Some example questions 07/12/2020 1) A steel ball-bearing of mass 1. 3 x 10 -4 kg and radius 2. 0 mm is allowed to fall through water until it reaches terminal velocity. Calculate this terminal velocity if the viscosity of water is 1. 1 x 10 -3 N s m-2. V=22. 8 ms-1 2) Another steel ball-bearing of density 8000 kgm-3 and radius 1. 0 mm is allowed to fall through water until it reaches terminal velocity. Calculate this terminal velocity if the viscosity of water is 1. 1 x 10 -3 N s m-2. V=13. 9 ms-1

Force and Extension Consider a mass on a spring: 07/12/2020

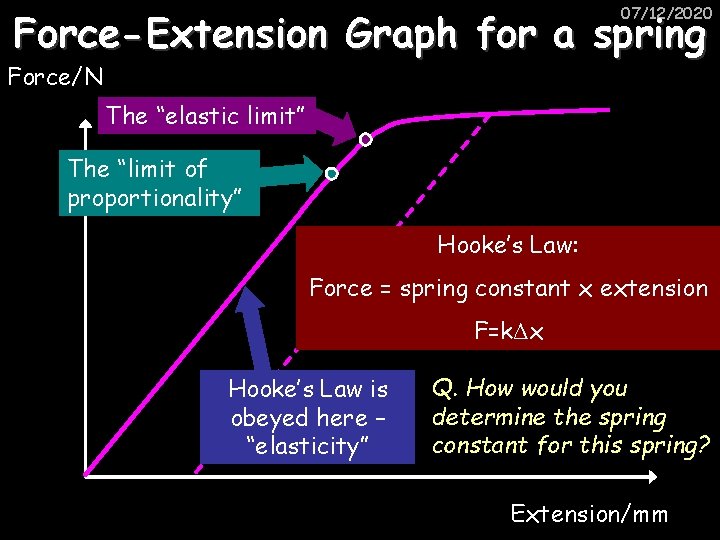
07/12/2020 Force-Extension Graph for a spring Force/N The “elastic limit” The “limit of proportionality” Hooke’s Law: Force = spring constant x extension F=kΔx Hooke’s Law is obeyed here – “elasticity” Q. How would you determine the spring constant for this spring? Extension/mm

07/12/2020 Questions on the Spring Constant 1) Estimate the spring constant of a 10 N Newton meter 2) Estimate the spring constant of the suspension on a car

Force and Extension Consider a mass on a spring: Putting a mass on a spring will extend it. Keep putting the masses on and the spring will stretch. Does this happen to other materials? 07/12/2020

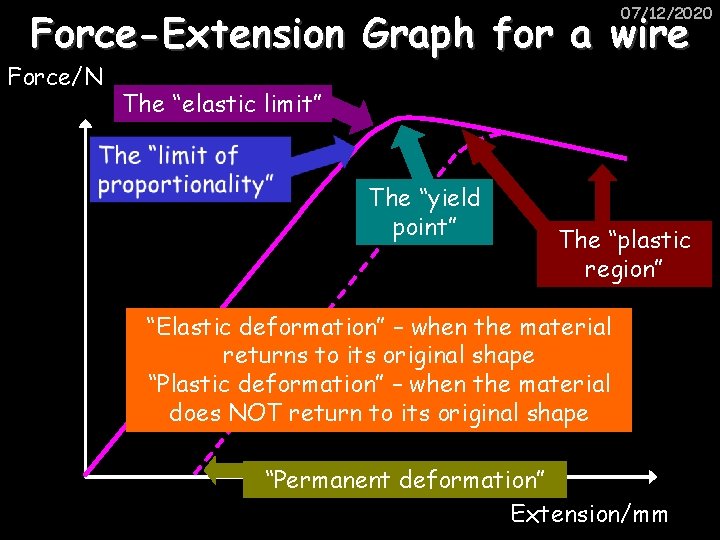
07/12/2020 Force-Extension Graph for a wire Force/N The “elastic limit” The “yield point” The “plastic region” “Elastic deformation” – when the material returns to its original shape “Plastic deformation” – when the material does NOT return to its original shape “Permanent deformation” Extension/mm

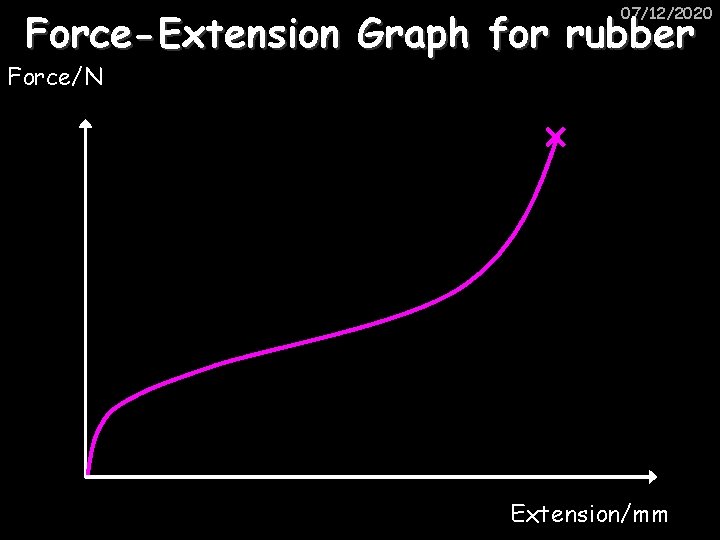
07/12/2020 Force-Extension Graph for rubber Force/N Extension/mm

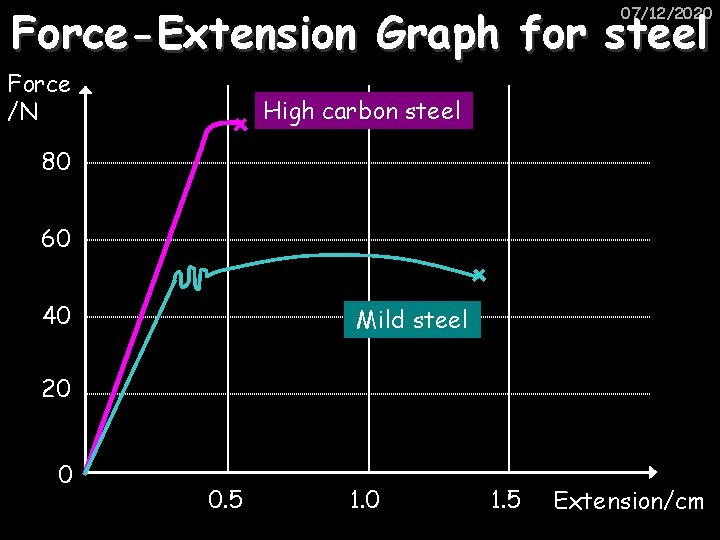
Force-Extension Graph for steel 07/12/2020 Force /N High carbon steel 80 60 40 Mild steel 20 0 0. 5 1. 0 1. 5 Extension/cm

Work done recap 07/12/2020 Work done (in joules) is simply the force needed to move an object multiplied by the distance moved in the direction of the force: ΔW ΔW = FΔs F Δs

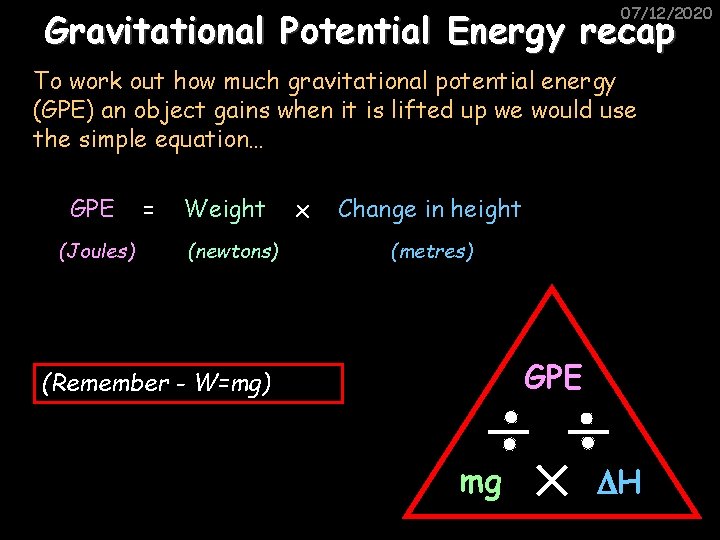
07/12/2020 Gravitational Potential Energy recap To work out how much gravitational potential energy (GPE) an object gains when it is lifted up we would use the simple equation… GPE (Joules) = Weight (newtons) x Change in height (metres) GPE (Remember - W=mg) mg H

Kinetic energy recap 07/12/2020 Any object that moves will have kinetic energy. The amount of kinetic energy an object has can be found using the formula: Kinetic energy = ½ x mass x velocity squared in J in kg Ek = ½ in m/s mv 2

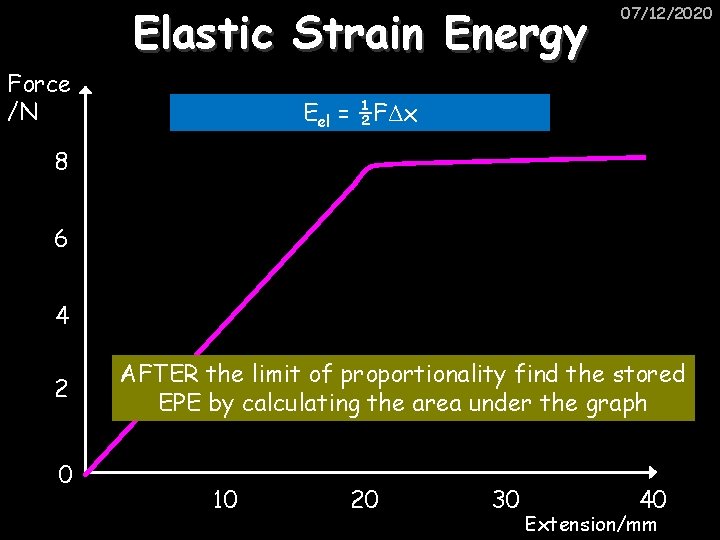
Elastic Strain Energy Force /N 07/12/2020 Eel = ½FΔx 8 6 4 2 0 AFTER the limit of proportionality find the stored EPE by calculating the area under the graph 10 20 30 40 Extension/mm

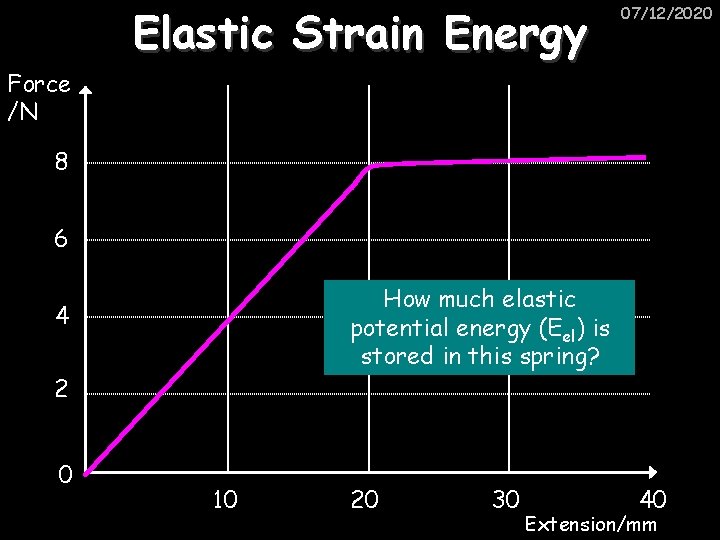
Elastic Strain Energy 07/12/2020 Force /N 8 6 How much elastic potential energy (Eel) is stored in this spring? 4 2 0 10 20 30 40 Extension/mm

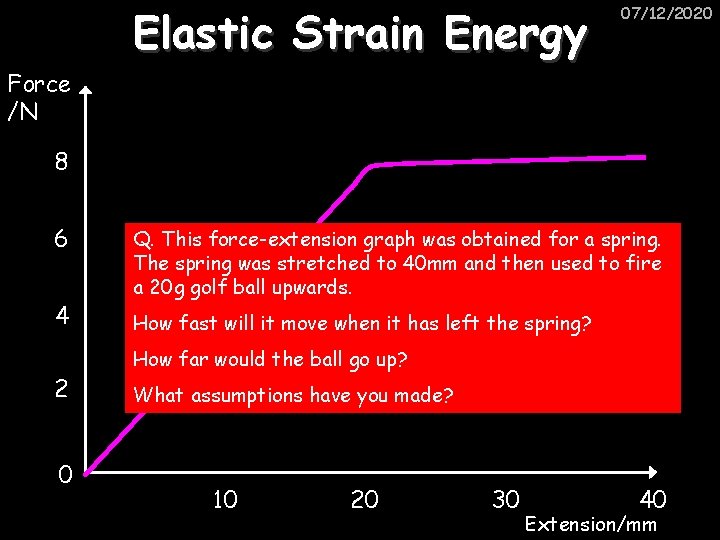
Elastic Strain Energy 07/12/2020 Force /N 8 6 4 2 0 Q. This force-extension graph was obtained for a spring. The spring was stretched to 40 mm and then used to fire a 20 g golf ball upwards. How fast will it move when it has left the spring? How far would the ball go up? What assumptions have you made? 10 20 30 40 Extension/mm

Practical – Using Catapults 07/12/2020 Task – to find out (mathematically) how far you would stretch a rubber band in order for it to “just” reach the ceiling and then test your theory! Step 1 – Obtain an F-Δs graph for your rubber band Step 2 – Calculate the total stored elastic potential energy at different extensions Step 3 – Choose your rubber to fire and measure its mass Step 4 – Use a calculation to predict how far up the object will go: Elastic potential energy = Gravitational potential energy EPE = mgh

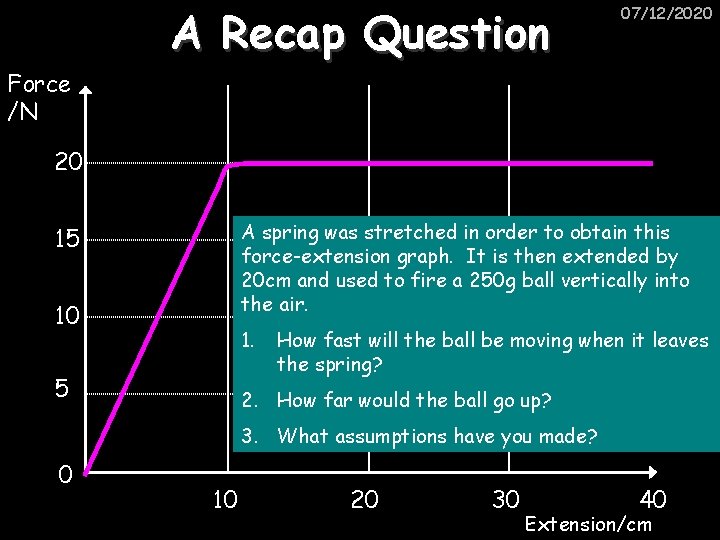
A Recap Question 07/12/2020 Force /N 20 A spring was stretched in order to obtain this force-extension graph. It is then extended by 20 cm and used to fire a 250 g ball vertically into the air. 15 10 1. 5 How fast will the ball be moving when it leaves the spring? 2. How far would the ball go up? 3. What assumptions have you made? 0 10 20 30 40 Extension/cm

Stress and Strain 07/12/2020 “Stress” means how much force per unit area a material is having put on it. Stress = force cross-sectional area σ=F A “Strain” means how much the material extends per unit length. Strain = extension original length ε = Δl l

The Young Modulus 07/12/2020 The Young Modulus for a material is defined as the following: Young modulus = stress strain From the last slide: Therefore: σ=F A and ε = Δl l Young modulus = Fl AΔl Q. A steel wire of length 3 m and diameter 0. 3 mm is extended by a force of 50 N. The wire extends by 2 mm. Calculate: 1) The applied stress 2) The strain on the wire 3) The Young Modulus of the steel

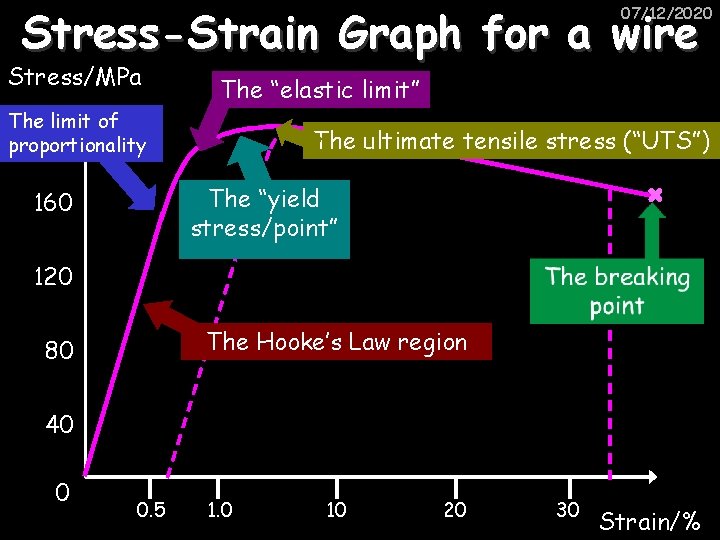
Stress-Strain Graph for a wire 07/12/2020 Stress/MPa The “elastic limit” The limit of 200 proportionality The ultimate tensile stress (“UTS”) The “yield stress/point” 160 120 The Hooke’s Law region 80 40 0 0. 5 1. 0 10 20 30 Strain/%

Force and compression 07/12/2020 Consider some springs: The force-compression and stress-strain graphs for objects like these can be determined and plotted. Example questions: 1) A stiff spring has a spring constant of 10 Nm-1. How much will it compress by if a force of 20 N is applied to it? 2) Estimate the stress on the lower bones in your leg when you are standing up.

Micrometers 07/12/2020 Micrometers are more accurate and can be used to measure the width or depth of an object to an accuracy of 0. 01 mm…

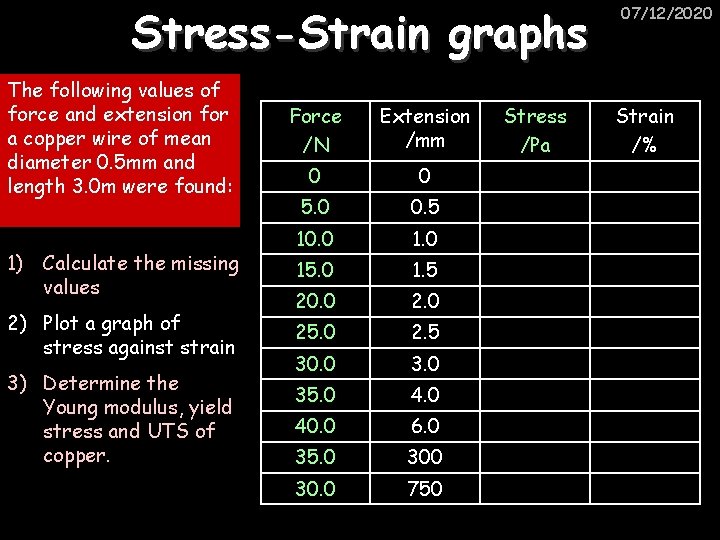
Stress-Strain graphs The following values of force and extension for a copper wire of mean diameter 0. 5 mm and length 3. 0 m were found: 1) Calculate the missing values 2) Plot a graph of stress against strain 3) Determine the Young modulus, yield stress and UTS of copper. Force /N Extension /mm 0 0 5. 0 0. 5 10. 0 15. 0 1. 5 20. 0 25. 0 2. 5 30. 0 35. 0 40. 0 6. 0 35. 0 30. 0 750 Stress /Pa 07/12/2020 Strain /%

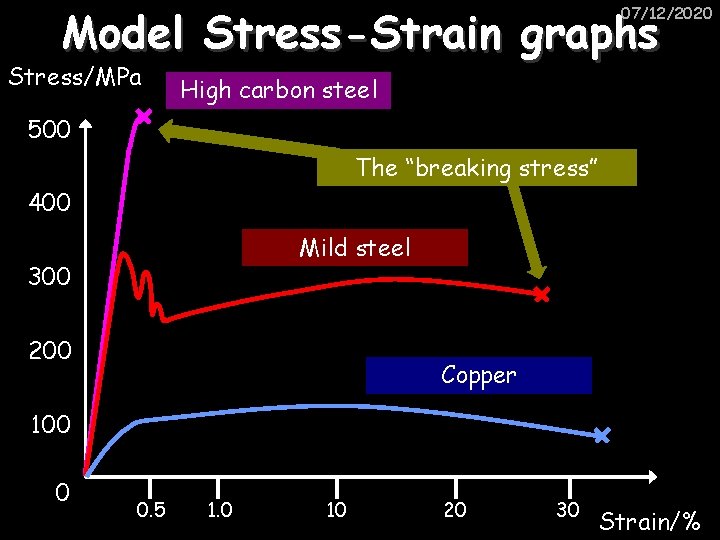
Model Stress-Strain graphs 07/12/2020 Stress/MPa High carbon steel 500 The “breaking stress” 400 Mild steel 300 200 Copper 100 0 0. 5 1. 0 10 20 30 Strain/%
 Dvt triangle physics
Dvt triangle physics Comparing distance/time graphs to speed/time graphs
Comparing distance/time graphs to speed/time graphs Calculating time with distance and speed
Calculating time with distance and speed Speed distance and time
Speed distance and time How to calculate speed by distance and time
How to calculate speed by distance and time Calculating speed time and distance worksheet
Calculating speed time and distance worksheet Speed distance and time
Speed distance and time Time speed distance triangle
Time speed distance triangle Speed distance and time
Speed distance and time The relationship among speed distance and time is
The relationship among speed distance and time is Speed time distance equation
Speed time distance equation Navigation using speed, distance and time calculations
Navigation using speed, distance and time calculations Distance formula time speed
Distance formula time speed Formula for speed distance and time
Formula for speed distance and time Distance = speed x time
Distance = speed x time Constant speed on distance time graph
Constant speed on distance time graph Distance, speed time triangle
Distance, speed time triangle Speed time distance triangle
Speed time distance triangle Distance traveled per unit time
Distance traveled per unit time Gcse speed distance time questions
Gcse speed distance time questions What two measurements are necessary for calculating speed
What two measurements are necessary for calculating speed Speed distance time gcse maths
Speed distance time gcse maths D=vt
D=vt Dr frost speed distance time
Dr frost speed distance time Calculating speed
Calculating speed Revision passive
Revision passive What is the difference of distance and displacement
What is the difference of distance and displacement Passengers can help a driver manage emotions by
Passengers can help a driver manage emotions by Speed detection of moving vehicle
Speed detection of moving vehicle Start time end time and elapsed time
Start time end time and elapsed time Velocity
Velocity What's the difference between speed and acceleration
What's the difference between speed and acceleration Speed is the ratio of the distance an object moves to *
Speed is the ratio of the distance an object moves to * The ratio of input distance to output distance
The ratio of input distance to output distance Speed and agility frequency, intensity, time type
Speed and agility frequency, intensity, time type Slant range dme
Slant range dme Distance and time graph
Distance and time graph Velocity time distance triangle
Velocity time distance triangle Creating and interpreting distance time graph
Creating and interpreting distance time graph Graphing speed
Graphing speed 65mph to ft/s
65mph to ft/s Velocity time graph
Velocity time graph Stationary motion graph
Stationary motion graph Ms-1
Ms-1 Time x speed
Time x speed Time distance shielding
Time distance shielding Distance rate time formula
Distance rate time formula Interpreting distance time graphs
Interpreting distance time graphs Time distance graph
Time distance graph Distance decay vs time space compression
Distance decay vs time space compression Distance divided by time
Distance divided by time Classic math problems
Classic math problems How to find average speed
How to find average speed Distance-time graph story match
Distance-time graph story match Time distance decay definition
Time distance decay definition Speed, velocity and acceleration quiz
Speed, velocity and acceleration quiz Distance-time graph worksheet doc
Distance-time graph worksheet doc Latin america city model
Latin america city model Distance time graph
Distance time graph Real life graphs
Real life graphs Force x distance / time
Force x distance / time Distance time graph for uniform motion
Distance time graph for uniform motion Distance time graph
Distance time graph Non linear distance time graphs
Non linear distance time graphs Wjec hospitality and catering revision
Wjec hospitality and catering revision Crime and deviance sociology revision
Crime and deviance sociology revision Romeo and juliet revision notes
Romeo and juliet revision notes General revision of assessments and property classification
General revision of assessments and property classification Crime and punishment revision guide
Crime and punishment revision guide Present continuous function
Present continuous function Romeo and juliet revision booklet
Romeo and juliet revision booklet Power and conflict revision booklet
Power and conflict revision booklet Jekyll and hyde revision
Jekyll and hyde revision Catering revision
Catering revision A level english language frameworks
A level english language frameworks Bcs infrastructure technician
Bcs infrastructure technician Revision present simple and continuous
Revision present simple and continuous Setup time and hold time in digital electronics
Setup time and hold time in digital electronics Ordinary and exact interest formula
Ordinary and exact interest formula Calculating infusion time and completion time calculator
Calculating infusion time and completion time calculator Seektime
Seektime Work study procedure
Work study procedure Standard time and normal time
Standard time and normal time Year 8 spanish revision booklet
Year 8 spanish revision booklet Place value revision
Place value revision Revision passive voice
Revision passive voice Revision.english.outwood
Revision.english.outwood Gcse pe revision booklet
Gcse pe revision booklet Criminology unit 4 crime and punishment
Criminology unit 4 crime and punishment Unit 4 criminology revision
Unit 4 criminology revision Criminology wjec unit 4
Criminology wjec unit 4 Virginia work area protection manual 2019
Virginia work area protection manual 2019 @ben1232323:the owner of a building
@ben1232323:the owner of a building What is revising?
What is revising? Iso 14001 revision
Iso 14001 revision Social class sailmaker
Social class sailmaker Sailmaker by alan spence
Sailmaker by alan spence Sailmaker play
Sailmaker play Safety at street works and road works a code of practice
Safety at street works and road works a code of practice What s your hobby
What s your hobby Revision unit 6
Revision unit 6 Revision image
Revision image Objective of revision
Objective of revision Science revision quiz
Science revision quiz 64:2³=2n
64:2³=2n Mrcgp question bank
Mrcgp question bank Before reported speech
Before reported speech Revisión fundamental
Revisión fundamental Recurso de reconsideración anses modelo
Recurso de reconsideración anses modelo Revision passive voice answer
Revision passive voice answer Past simple kako se gradi
Past simple kako se gradi Othello freytag pyramid
Othello freytag pyramid Ocr cambridge technicals level 3 sport unit 3 revision
Ocr cambridge technicals level 3 sport unit 3 revision Ruae revision
Ruae revision Theorems of euclidean geometry
Theorems of euclidean geometry Utilerías de revisión
Utilerías de revisión Igcse tips
Igcse tips Igcse ict revision notes
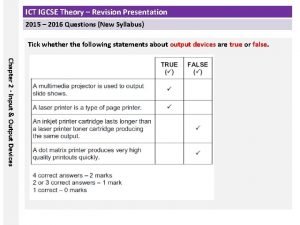
Igcse ict revision notes Ict igcse theory revision presentation
Ict igcse theory revision presentation Ict chapter 4
Ict chapter 4 Ict igcse theory revision presentation
Ict igcse theory revision presentation Ib psychology revision
Ib psychology revision Gcse maths revision ppt
Gcse maths revision ppt Geography paper 2 revision notes
Geography paper 2 revision notes Describe watershed
Describe watershed Edexcel geography gcse checklist
Edexcel geography gcse checklist Fsmq
Fsmq Dr faustus revision
Dr faustus revision Pasos de la revision de la literatura
Pasos de la revision de la literatura Make me a revision timetable
Make me a revision timetable Forces revision poster
Forces revision poster Product design revision
Product design revision Themes of a christmas carol
Themes of a christmas carol Ggbs is code 16714
Ggbs is code 16714 Vdot wapm revision 2
Vdot wapm revision 2 Year 6 sats revision timetable
Year 6 sats revision timetable Virtue ethics revision
Virtue ethics revision Revision invitation to party
Revision invitation to party Our class won the competition
Our class won the competition John brushes his teeth
John brushes his teeth Forgetting curve revision timetable
Forgetting curve revision timetable Nat 5 maths pythagoras
Nat 5 maths pythagoras Bubble he assessment
Bubble he assessment Scratch revision
Scratch revision Making a revision timetable
Making a revision timetable Translation
Translation Revision part 1
Revision part 1 Adverbs of frequency exercises
Adverbs of frequency exercises Raleigh's letter journey's end
Raleigh's letter journey's end Presetination
Presetination Gcse maths revision ppt
Gcse maths revision ppt Higher biology unit 3 revision
Higher biology unit 3 revision How useful is this source
How useful is this source Geography paper 1 case studies aqa
Geography paper 1 case studies aqa Gcse catering revision
Gcse catering revision Engineering revision guide
Engineering revision guide Edexcel gcse english literature past papers
Edexcel gcse english literature past papers Creative i media revision
Creative i media revision Conditionals revision
Conditionals revision Sql bbc bitesize
Sql bbc bitesize Complex numbers revision
Complex numbers revision Context for bayonet charge
Context for bayonet charge Food technology revision
Food technology revision