07 January 2022 Drawing a graph from a

07 January 2022 Drawing a graph from a table of values LO: Use a table of values to calculate the coordinates of the points to draw a graph. www. mathssupport. org

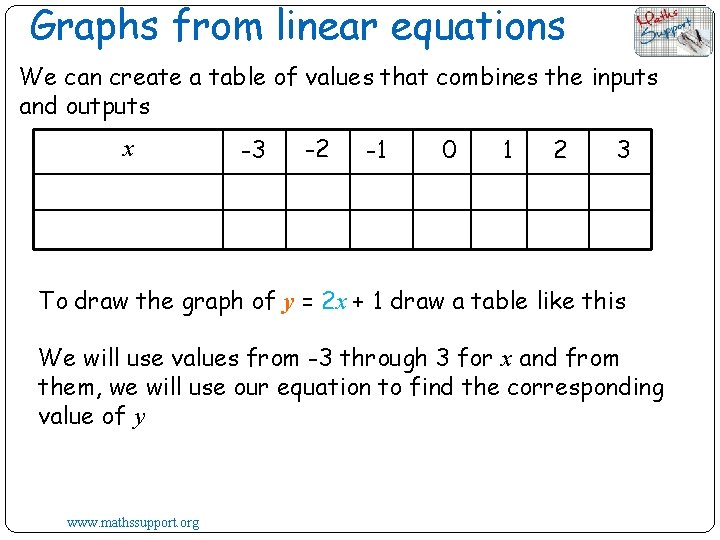
Graphs from linear equations In this section we are going to graph some straight lines from tables of values. Consider the equation: y = 2 x + 1 We can choose any value we like for x and use our equation to find the corresponding value of y www. mathssupport. org

Graphs from linear equations We can create a table of values that combines the inputs and outputs x -3 -2 -1 0 1 2 3 To draw the graph of y = 2 x + 1 draw a table like this We will use values from -3 through 3 for x and from them, we will use our equation to find the corresponding value of y www. mathssupport. org

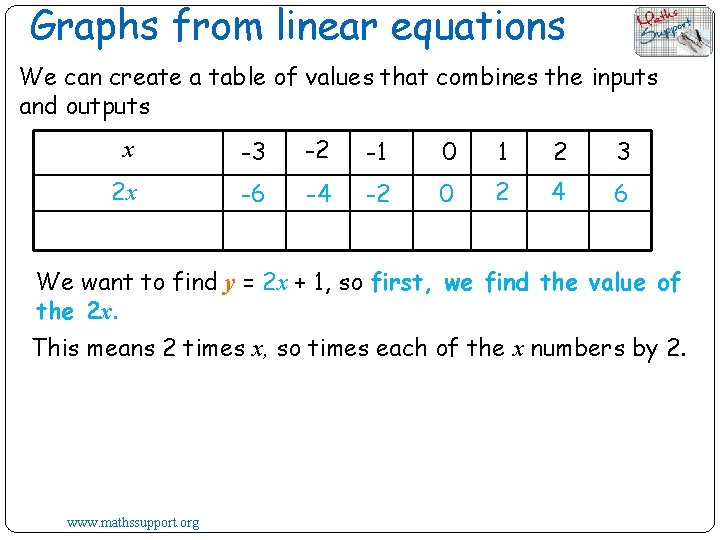
Graphs from linear equations We can create a table of values that combines the inputs and outputs x -3 -2 -1 0 1 2 3 2 x -6 -4 -2 0 2 4 6 We want to find y = 2 x + 1, so first, we find the value of the 2 x. This means 2 times x, so times each of the x numbers by 2. www. mathssupport. org

Graphs from linear equations We can create a table of values that combines the inputs and outputs x -3 -2 -1 0 1 2 3 2 x -6 -4 -2 0 2 4 6 -5 -3 -1 1 3 5 7 y = 2 x + 1 Since we want to find y = 2 x + 1, so now we add on 1 all the values of 2 x to get the value of y. www. mathssupport. org

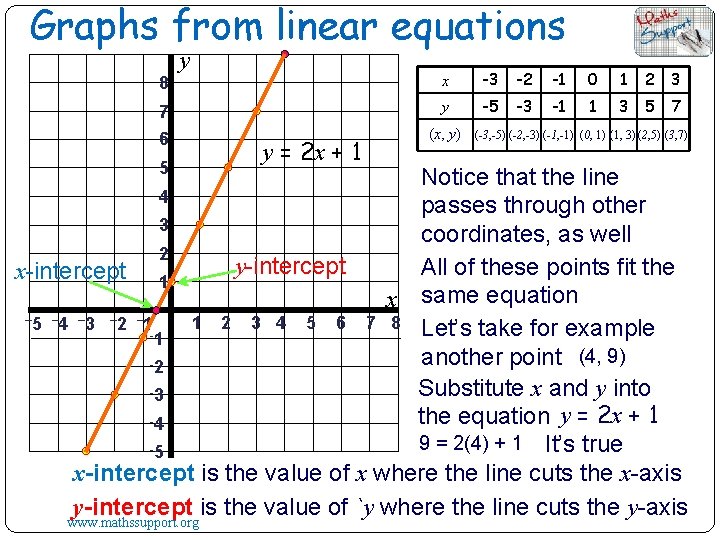
Graphs from linear equations We can create a table of values that combines the inputs and outputs x -3 -2 -1 0 1 2 3 2 x -6 -4 -2 0 2 4 6 -5 -3 -1 1 3 5 7 y = 2 x + 1 (x, y) (-3, -5) (-2, -3) (-1, -1) (0, 1) (1, 3) (2, 5) (3, 7) Now that we have found the y number y = 2 x + 1. We have the coordinate pairs to plot on the grid www. mathssupport. org

Graphs from linear equations y 8 x -3 -2 -1 0 1 2 3 7 y -5 -3 -1 1 3 5 7 6 (x, y) 5 y = 2 x + 1 (-3, -5) (-2, -3) (-1, -1) (0, 1) (1, 3) (2, 5) (3, 7) Notice that the line 4 passes through other 3 coordinates, as well 2 y-intercept All of these points fit the x-intercept 1 x same equation – 5 – 4 – 3 – 2 – 1 1 2 3 4 5 6 7 8 Let’s take for example -1 another point (4, 9) -2 Substitute x and y into -3 the equation y = 2 x + 1 -4 9 = 2(4) + 1 It’s true -5 x-intercept is the value of x where the line cuts the x-axis y-intercept is the value of `y where the line cuts the y-axis www. mathssupport. org

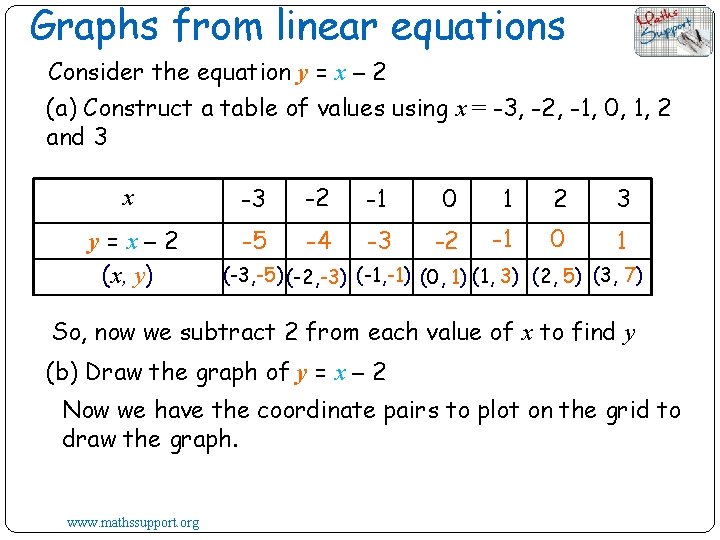
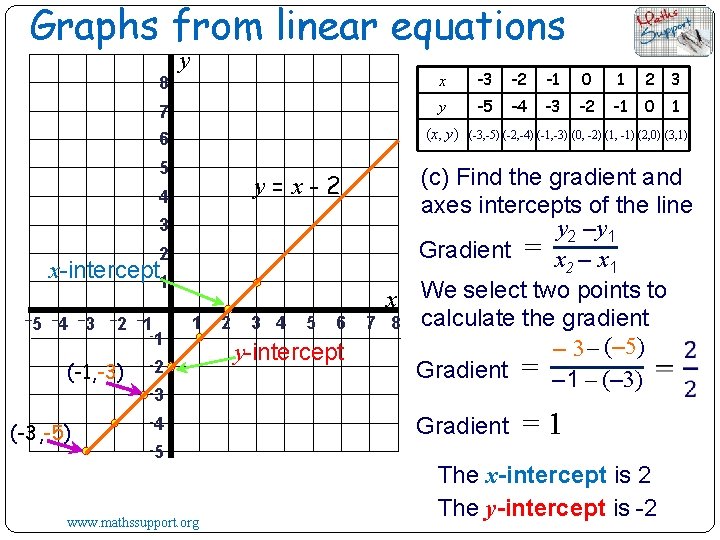
Graphs from linear equations Consider the equation y = x – 2 (a) Construct a table of values using x = -3, -2, -1, 0, 1, 2 and 3 x -3 -2 -1 0 1 2 3 y=x– 2 (x, y) -5 -4 -3 -2 -1 0 1 (-3, -5) (-2, -3) (-1, -1) (0, 1) (1, 3) (2, 5) (3, 7) So, now we subtract 2 from each value of x to find y (b) Draw the graph of y = x – 2 Now we have the coordinate pairs to plot on the grid to draw the graph. www. mathssupport. org

Graphs from linear equations y 8 x -3 -2 -1 0 1 2 3 7 y -5 -4 -3 -2 -1 0 1 6 (x, y) 5 y=x-2 4 3 2 x-intercept 1 – 5 – 4 – 3 – 2 – 1 -1 (-1, -3) 1 -2 -3 (-3, -5) -4 -5 www. mathssupport. org 2 3 4 5 6 y-intercept 7 (-3, -5) (-2, -4) (-1, -3) (0, -2) (1, -1) (2, 0) (3, 1) (c) Find the gradient and axes intercepts of the line y 2 –y 1 Gradient = x – x 2 1 x We select two points to 8 calculate the gradient – 3 – (– 5) Gradient = – 1 – (– 3) Gradient =1 The x-intercept is 2 The y-intercept is -2

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www. mathssupport. org