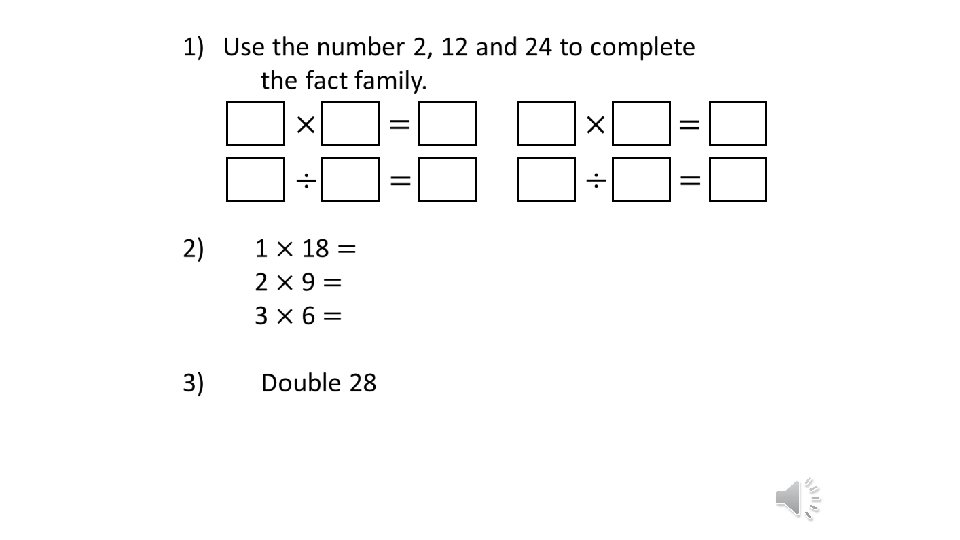
07 01 21 L O To identify factor










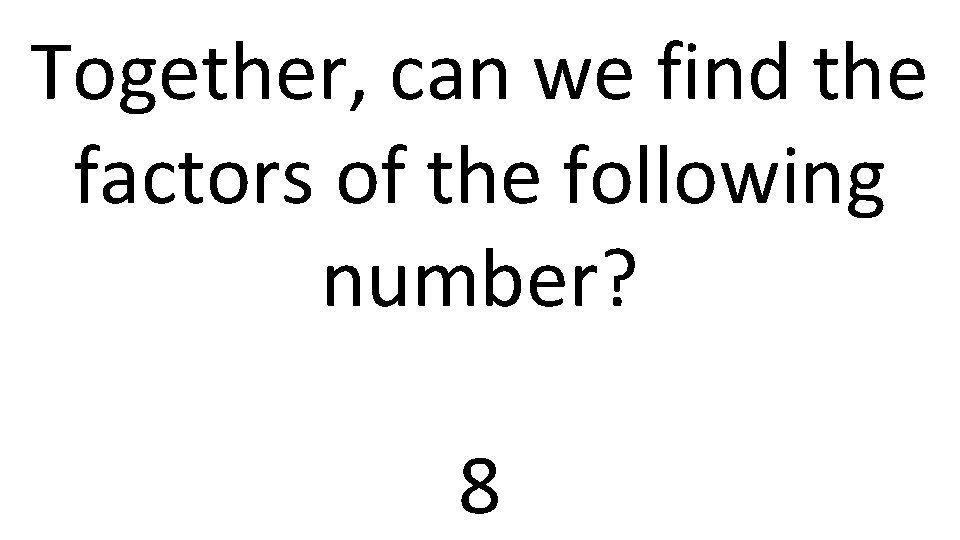








- Slides: 31

07. 01. 21 L. O: To identify factor pairs

Warm up…


2 12 24 12 2 24 2 12 18 18 18 56

07. 01. 21 L. O: To identify factor pairs Video link to support this lesson: https: //vimeo. com/491282075

What is a factor? What are the factors of 12? Well, it’s easier to think about factors as pairs. Think about the times table facts we know, where do we see the number 12? Where we see the number 12, the numbers in the multiplication sentence are a factor pair. For example, the factors of 12 are: 1 and 12 – 1 x 12= 12 or 12 x 1=12 2 and 6 – 2 x 6 = 12 0 r 6 x 2= 12 3 and 4 - 3 x 4 =- 12 or 4 x 3= 12 This means that the factors of 12 (in order) are 1, 2, 3, 4, 6 and 12. Writing factors in pairs helps to avoid missing out any numbers.

Two numbers multiplied create a product. Do some numbers have more than one factor? Yes! Think back to the factors or 12… we know the factors of 12 are: 1 and 12 – 1 x 12= 12 or 12 x 1 =12 2 and 6 – 2 x 6 = 12 0 r 6 x 2= 12 3 and 4 - 3 x 4 =- 12 or 4 x 3= 12 So numbers can have more than one factor.

Hot Tips: Factors always come in pairs 1 and the number itself will always be a factor of each number. Use your timetable knowledge!

What is a factor? factor 2 rows of 3 are equal to 6 2× 3=6 factor 3 columns of 2 are equal to 6 3 × 2 = 6 2 and 3 are factors of 6 Have a think Are there any other factors of 6? product

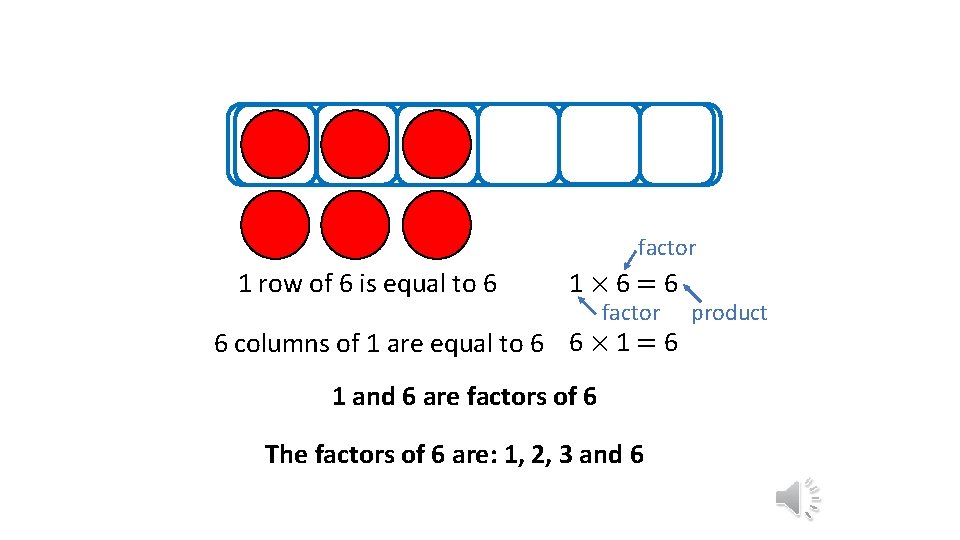
factor 1 row of 6 is equal to 6 1× 6=6 factor 6 columns of 1 are equal to 6 6 × 1 = 6 1 and 6 are factors of 6 The factors of 6 are: 1, 2, 3 and 6 product

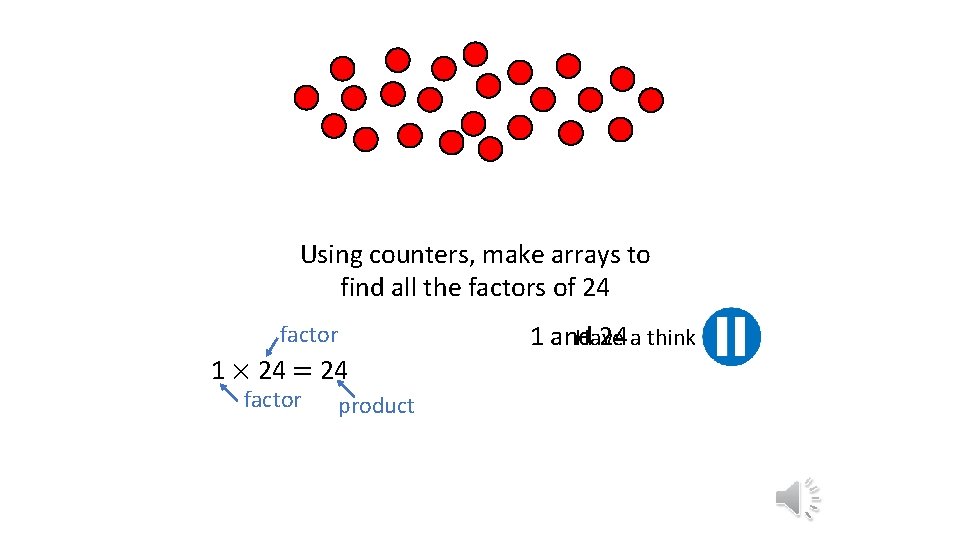
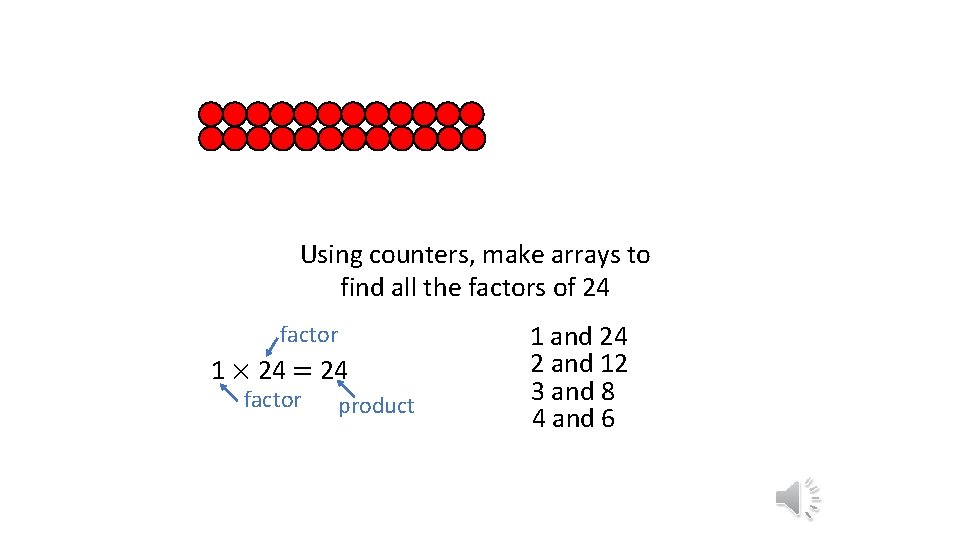
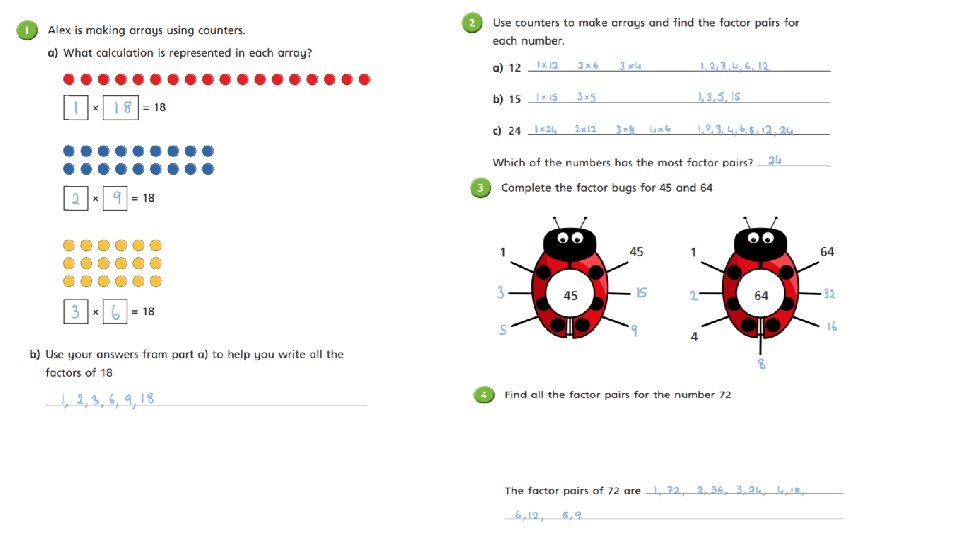
Using counters, make arrays to find all the factors of 24 factor 1 × 24 = 24 factor product Have 1 and 24 a think

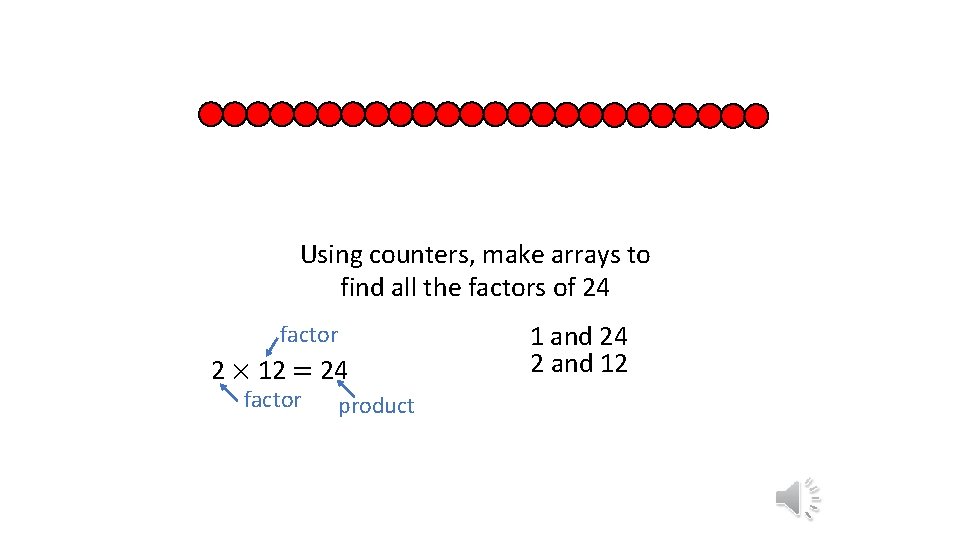
Using counters, make arrays to find all the factors of 24 factor 2 × 12 = 24 factor product 1 and 24 2 and 12

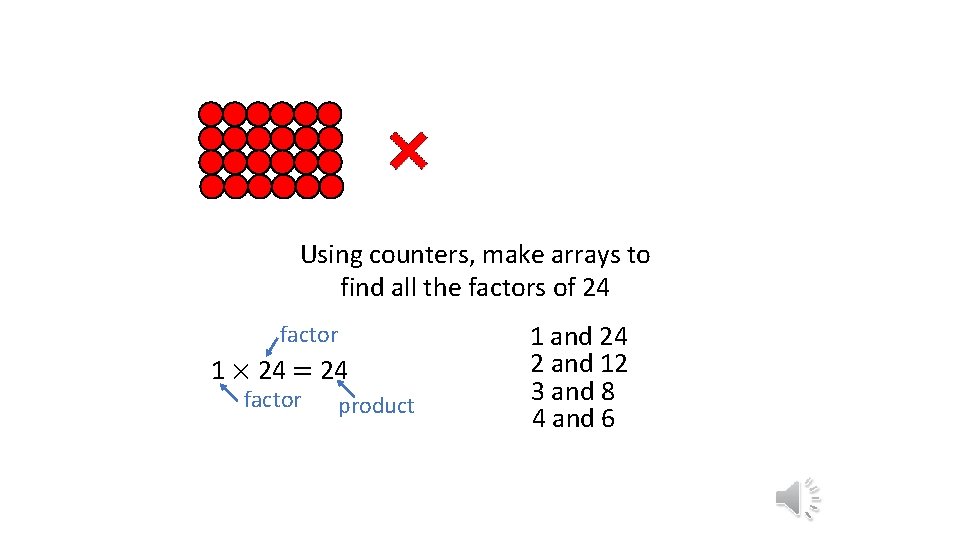
Using counters, make arrays to find all the factors of 24 factor 1 × 24 = 24 factor product 1 and 24 2 and 12 3 and 8 4 and 6

Using counters, make arrays to find all the factors of 24 factor 1 × 24 = 24 factor product 1 and 24 2 and 12 3 and 8 4 and 6

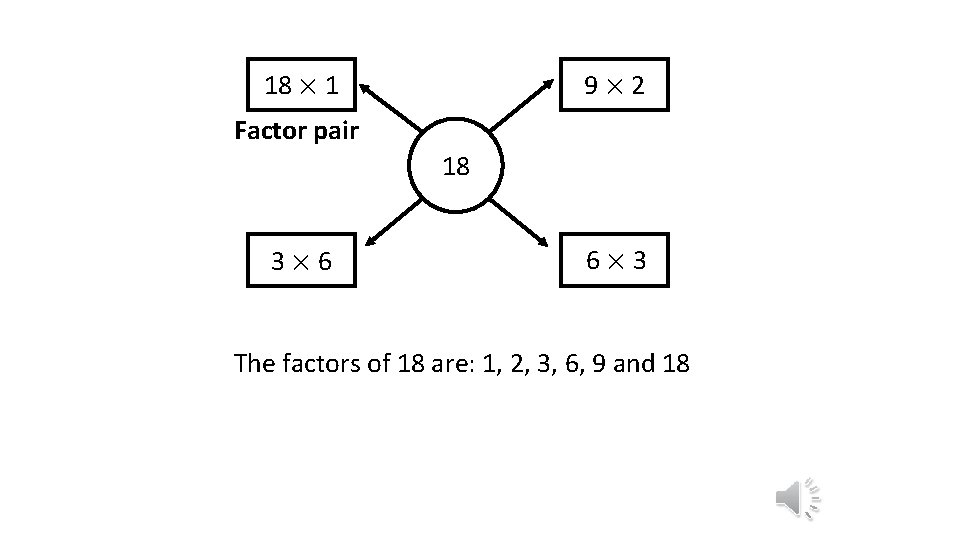
18 × 1 9× 2 Factor pair 18 3× 6 6× 3 The factors of 18 are: 1, 2, 3, 6, 9 and 18

Factors have to be integers (whole numbers). Have a think What are the factors of 5? 1 and 5

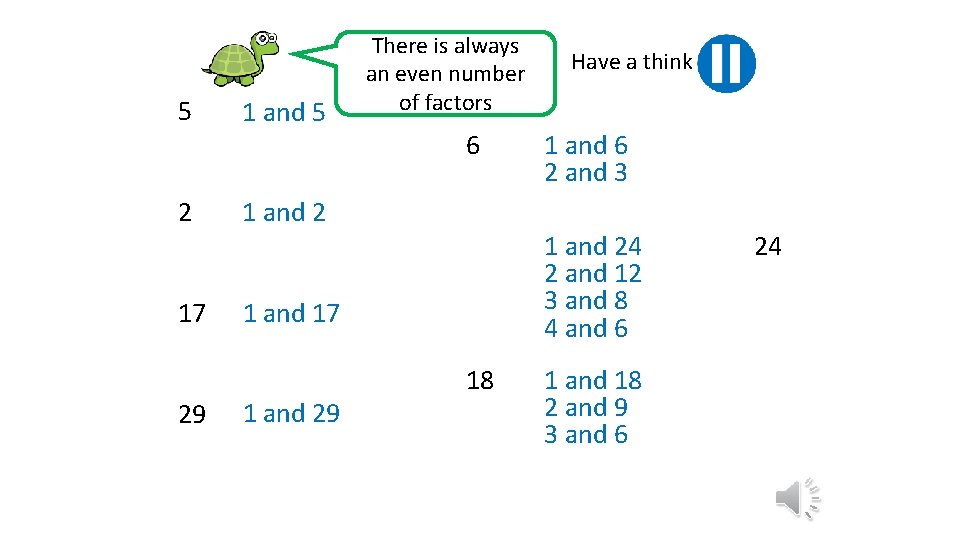
List the factors of these numbers: 5 1 and 5 2 1 and 2 17 1 and 17 29 1 and 29 Have a think What other numbers can you find with only have 2 factors? What do you notice? They all only have 2 factors

5 2 17 29 1 and 5 There is always an even number of factors 6 1 and 2 1 and 6 2 and 3 1 and 24 2 and 12 3 and 8 4 and 6 1 and 17 1 and 29 Have a think 18 1 and 18 2 and 9 3 and 6 24

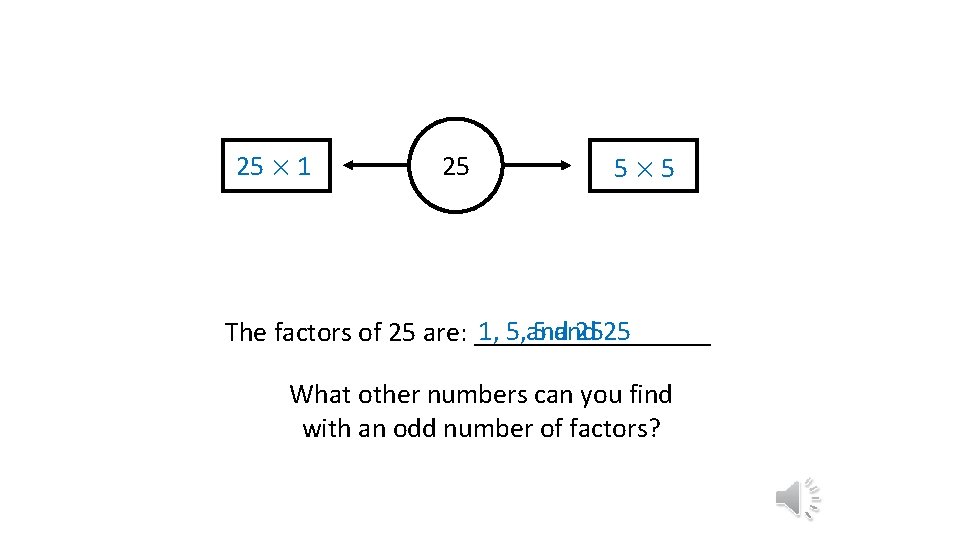
25 × 1 25 5× 5 1, 5 5, and 5 and 2525 The factors of 25 are: _________ What other numbers can you find with an odd number of factors?
Together, can we find the factors of the following number? 8

8 Firstly, we know all numbers have the factor pairs 1 and the number itself. So, here we know 1 and 8 are factors of 8. 8 is an even number so, we know 2 is a factor of 8. 2 x 4= 8 Therefore, 4 is also a factor of 8. The factors of 8 are: 1, 2, 4 and 8

Can you find a factor pair for each number? 15 24 36

Can you find a factor pair for each number? 12 24 44

Can you find a factor pair for each number? 18 24 48

Can you find a factor pair for each number? 16 36 72

Can you find a factor pair for each number? You might find it easier to write your answer as a multiplication sentence. For example: 18 = 9 x 2 4 8 6 25 30 70 18 28 35 45 60 100 12 18 60 27 36 70 24 54 33 45 14 28 54 66 27 32 70 88 72 48 35 28 63 If you fancy a challenge, can you find all of the factors for each number?



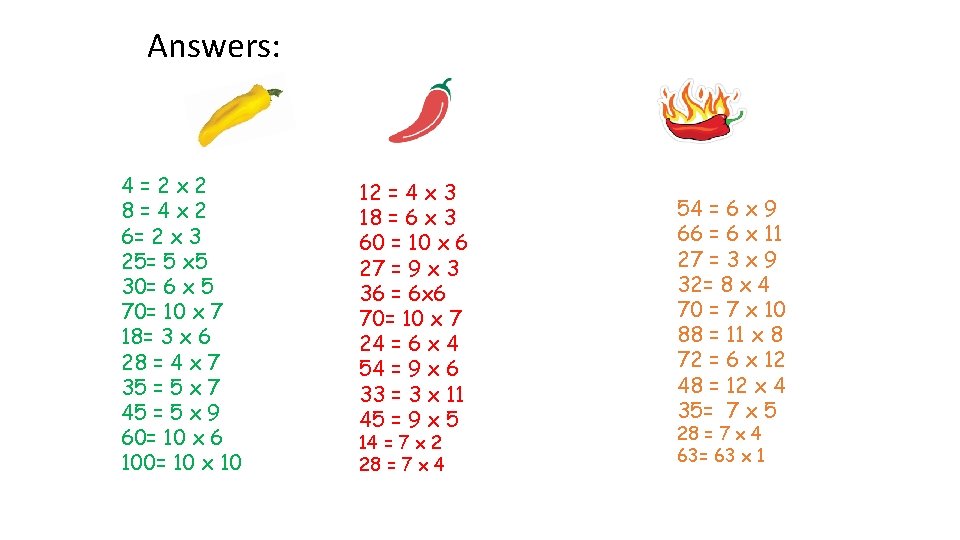
Answers: 4=2 x 2 8=4 x 2 6= 2 x 3 25= 5 x 5 30= 6 x 5 70= 10 x 7 18= 3 x 6 28 = 4 x 7 35 = 5 x 7 45 = 5 x 9 60= 10 x 6 100= 10 x 10 12 = 4 x 3 18 = 6 x 3 60 = 10 x 6 27 = 9 x 3 36 = 6 x 6 70= 10 x 7 24 = 6 x 4 54 = 9 x 6 33 = 3 x 11 45 = 9 x 5 14 = 7 x 2 28 = 7 x 4 54 = 6 x 9 66 = 6 x 11 27 = 3 x 9 32= 8 x 4 70 = 7 x 10 88 = 11 x 8 72 = 6 x 12 48 = 12 x 4 35= 7 x 5 28 = 7 x 4 63= 63 x 1

