06 Viewing Camera Imam Cholissodin imam cholissodingmail com

06 | Viewing / Camera Imam Cholissodin| imam. cholissodin@gmail. com

Viewing / Camera : 1. What’s Viewing / Camera 2. Parallel Projection 3. Parallel Projection Syntax 4. Perspective Projection 5. Perspective Projection Syntax 6. Activation Function 7. Multiple View 8. Taxonomy Projection 9. Math for Computer Graphics 10. Demos Program

What’s Viewing / Camera • Cara mengatur pandangan objek 2 D maupun 3 D dan mengontrol pergerakan kamera.

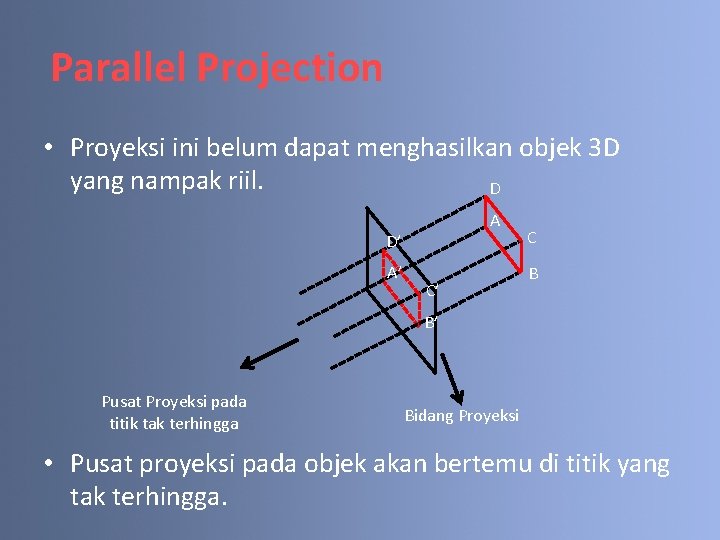
Parallel Projection • Proyeksi ini belum dapat menghasilkan objek 3 D yang nampak riil. D A D’ A’ C’ C B B’ Pusat Proyeksi pada titik tak terhingga Bidang Proyeksi • Pusat proyeksi pada objek akan bertemu di titik yang tak terhingga.

Parallel Projection Syntax • gl. Ortho(-15. 0, 20. 0, -10. 0, 15. 0, -50. 0, 70. 0); – Mendefinisikan besarnya sistem koordinat 3 D : dengan range sumbu x adalah [-15, 20], range untuk sumbu y adalah [-10, 15], range untuk sumbu z adalah [-50, 70] • glu. Ortho 2 D(-100, -200, 200); – Mendefinisikan besarnya sistem koordinat 2 D : dengan range sumbu x adalah [-100, 100] dan range untuk sumbu y adalah [-200, 200]

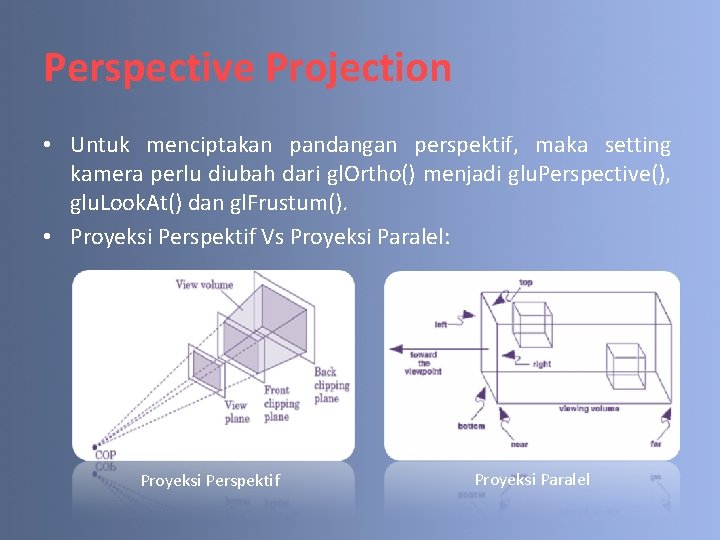
Perspective Projection • Untuk menciptakan pandangan perspektif, maka setting kamera perlu diubah dari gl. Ortho() menjadi glu. Perspective(), glu. Look. At() dan gl. Frustum(). • Proyeksi Perspektif Vs Proyeksi Paralel: Proyeksi Perspektif Proyeksi Paralel

Perspective Projection Syntax • glu. Perspective( GLdouble fovy, GLdouble aspect, GLdouble near, GLdouble far ) – fovy is the angle in the field of view (in range from [0. 0, 180]) – aspect is the aspect ratio of the frustrum (width of window over height of window) – near and far are the values between viewpoint and the near/far clipping planes

Perspective Projection Syntax • gl. Frustum( GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far ) – left, right, top, and bottom define the boundaries of the near clipping plane – near and far specify how far from the viewpoint the near and far clipping planes are

Perspective Projection Syntax • glu. Look. At( GLdouble e_x, GLdouble e_y, GLdouble e_z, GLdouble c_x, GLdouble c_y, GLdouble c_z, GLdouble u_x, GLdouble u_y, GLdouble u_z ) – e_x, e_y, and e_z specify the desired viewpoint (eye) – c_x, c_y, c_z specify some point along the desired line of sight (center) – u_x, u_y, and u_z define the up vector of our camera (up) note : glu. Look. At (Synthetic Camera)

Activation Function • glu. Perspective() : …………… gl. Matrix. Mode(GL_PROJECTION); gl. Load. Identity(); glu. Perspective(Angle. View, Aspek Rasio, Near, Far); ……………………. . • glu. Look. At() : …………… gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); glu. Look. At(mata_x, mata_y, mata_z, lihat_x, lihat_y, lihat_z, atas_x, atas_y, atas_z); ……………………. .

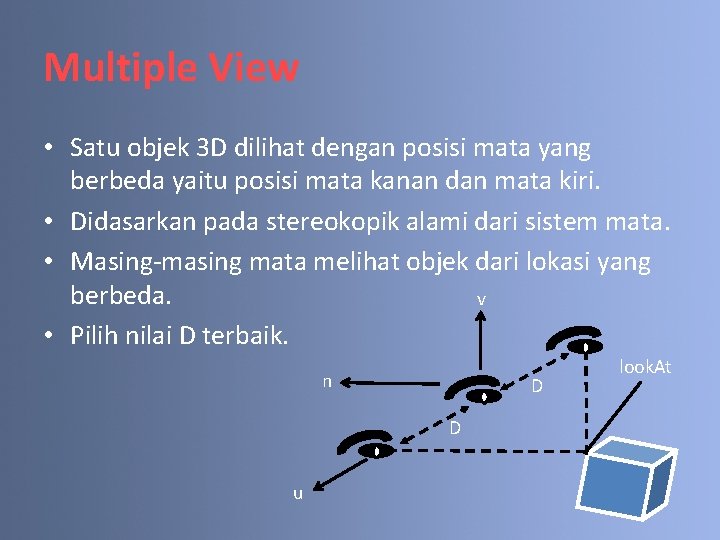
Multiple View • Satu objek 3 D dilihat dengan posisi mata yang berbeda yaitu posisi mata kanan dan mata kiri. • Didasarkan pada stereokopik alami dari sistem mata. • Masing-masing mata melihat objek dari lokasi yang berbeda. v • Pilih nilai D terbaik. n D D u look. At

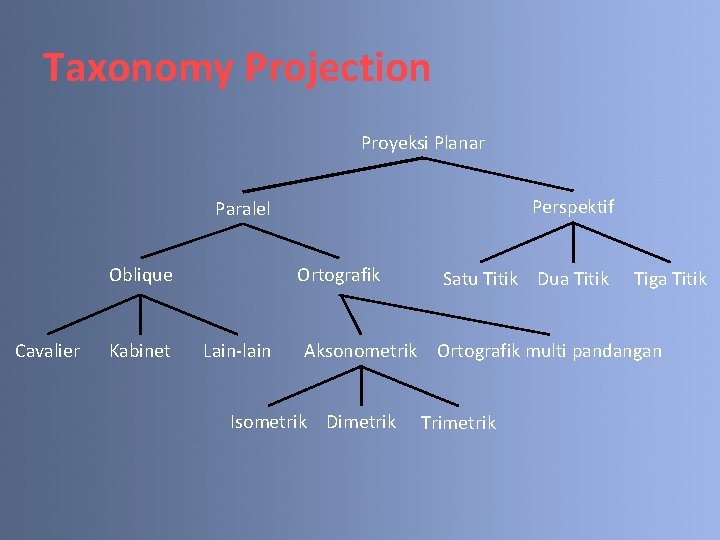
Taxonomy Projection Proyeksi Planar Perspektif Paralel Oblique Cavalier Kabinet Ortografik Lain-lain Satu Titik Dua Titik Tiga Titik Aksonometrik Ortografik multi pandangan Isometrik Dimetrik Trimetrik

Taxonomy Projection • Proyeksi Ortografik (Pandangan Aksonometrik) a) Isometrik : Semua sumbu x, y dan z diset dengan panjang yang sama. b) Dimetrik : Dua dari tiga sumbu koordinat diset dengan panjang yang sama. c) Trimetrik : Semua sumbu x, y dan z diset dengan tidak sama y panjang. y y x z (a) x x z (b) z (c)

Taxonomy Projection • Proyeksi Oblique (Kombinasi Ortografi) – Proyeksi ini mempertahankan muka objek dan memberikan kesan alami 3 D yang lebih baik. 1 1 Cavalier 1 3/4 1 2/3 1 Cabinet 1/2

Math for Computer Graphics Vektor Sistem Koordinat Homogen Translasi 2 D dan 3 D Skala 2 D dan 3 D Rotasi 2 D dan 3 D Kombinasi Transformasi (Misal objek 2 D : Translasi -> Rotasi -> Skala) • Math of Synthetic Camera • • •

Vektor • Titik 2 D -> Vektor 3 D -> Matrik 3 D -> Vektor 3 D (Px, Py) -> [Px Py 1] -> Matrik 3 D -> [Qx Qy 1] • Titik 3 D -> Vektor 4 D -> Matrik 4 D -> Vektor 4 D (Px, Py, Pz)->[Px Py Pz 1] -> Matrik 4 D -> [Qx Qy Qz 1]

Vektor • Vektor adalah kumpulan nilai yang memiliki besaran dan arah. • Operasi vektor : +, Contoh : u + v , v - u • Kombinasi vektor : – Kombinasi Linier (a 1 u + a 2 v) – Kombinasi Affine Jumlah semua komponennya 1. (a 1+a 2+…+an=1) – Kombinasi Konvek Jumlah semua komponen 1, tetapi semua nilai koefisiennya adalah 0 ≤ ai ≤ 1. (a 1+a 2+…+an=1)

Vektor • Besar Vektor Jika vektor u=(2, 2, 1), maka |u|= √(22+22+12)= √ 9 = 3 • Dot Product a • b=|a||b|cos Ө a Ө b Contoh : Diketahui dua buah vektor a=[2 3] dan b=[3 -1], carilah sudut antara a dan b ! Jawab : |a|= √ 22+32= √ 13=3. 6 dan |b|= √ 32+(-1)2= √ 10=3. 16 Unit Vektor : Ua = a/|a| = [2 3]/3. 6 = [0. 55 0. 16] normalisasi vektor, |Ua|=|Ub|=1 Ub = b/|b| = [3 -1]/3. 16 = [0. 95 0. 32] cos Ө = Ua. Ub = (0. 55 x 0. 95) + (0. 16 x 0. 32) = 0. 52 + 0. 05 = 0. 57 Jadi Ө = arccos (0. 57) = 55. 280

Vektor • Cross Product |axb|=|a||b|sin Ө a axb b • Contoh : Diketahui dua buah vektor a = [3 3 1] dan b =[2 2 -3]. Carilah vektor yang tegak lurus terhadap a dan b. Jawab :

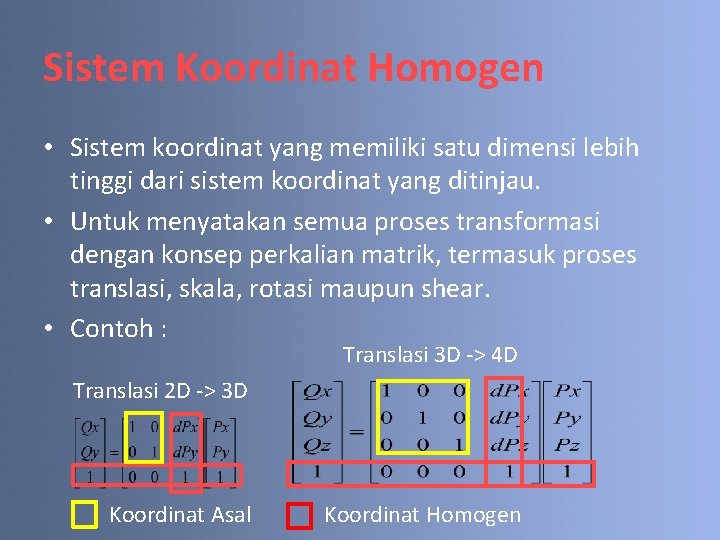
Sistem Koordinat Homogen • Sistem koordinat yang memiliki satu dimensi lebih tinggi dari sistem koordinat yang ditinjau. • Untuk menyatakan semua proses transformasi dengan konsep perkalian matrik, termasuk proses translasi, skala, rotasi maupun shear. • Contoh : Translasi 3 D -> 4 D Translasi 2 D -> 3 D Koordinat Asal Koordinat Homogen

Translasi 2 D • Tentukan matrik translasi M untuk memindakan titik P(4, 6) ke Q=(10, 3) ! Jawab : d. Px = 10 -4 = 6 dan d. Py = 3 -6 = -3 Jadi matrik translasi M adalah

Translasi 3 D • Tentukan matrik translasi M untuk memindahkan titik P=(4, 6, 2) ke Q=(10, 3, 5) ! Jawab : d. Px = 10 -4 = 6, d. Py = 3 -6 = -3, d. Pz = 5 -2 = 3 Jadi matrik translasi M adalah

Skala 2 D • Tentukan matrik skala untuk menskala titik P=(6, 2) ke Q=(3, 4). Jawab : s. Px = 3/6 = 1/2 dan s. Py = 4/2 = 2 Jadi matrik skala adalah

Skala 3 D • Tentukan matrik skala untuk menskala titik P=(6, 2, 9) ke Q=(3, 4, 3) Jawab : s. Px = 3/6 = 1/2, s. Py = 4/2 = 2, s. Pz = 3/9 = 1/3 Jadi matrik skala adalah

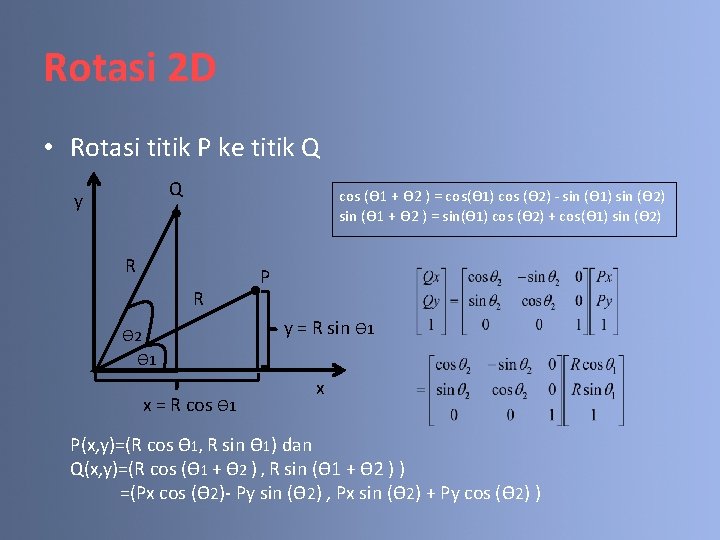
Rotasi 2 D • Rotasi titik P ke titik Q Q y cos (Ө 1 + Ө 2 ) = cos(Ө 1) cos (Ө 2) - sin (Ө 1) sin (Ө 2) sin (Ө 1 + Ө 2 ) = sin(Ө 1) cos (Ө 2) + cos(Ө 1) sin (Ө 2) R R Ө 2 Ө 1 x = R cos Ө 1 P y = R sin Ө 1 x P(x, y)=(R cos Ө 1, R sin Ө 1) dan Q(x, y)=(R cos (Ө 1 + Ө 2 ) , R sin (Ө 1 + Ө 2 ) ) =(Px cos (Ө 2)- Py sin (Ө 2) , Px sin (Ө 2) + Py cos (Ө 2) )

Rotasi 2 D • Tentukan rotasikan titik P=(3, 2) dengan sudut rotasi 30 derajat. Jawab : Qx = 3/6 = 1/2 dan Qy = 4/2 = 2 Q(x, y)=(3 cos (30) - 2 sin (30) , 3 sin (30) + 2 cos (30) ) =(3(0. 86)-2(0. 5) , 3(0. 5)+2(0. 86)) =((2. 58 - 1) , (1. 5+1. 72)) =(1. 58, 3. 22)

Rotasi 2 D • Rotation about an arbitrary axis (Rotasi pada sembarang sumbu (Xr, Yr) dengan sudut Ө)

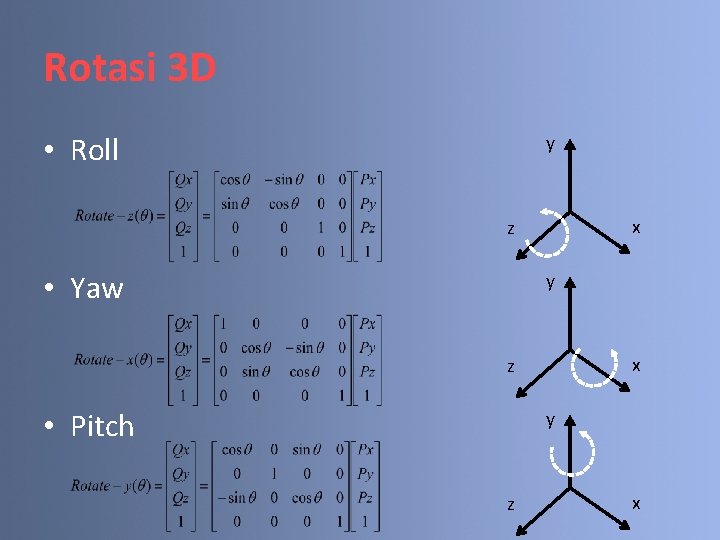
Rotasi 3 D • Roll y x z • Yaw y x z y • Pitch z x

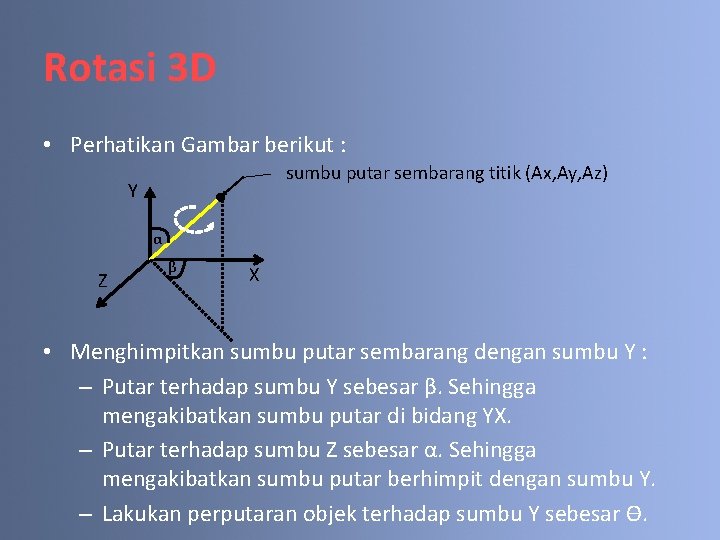
Rotasi 3 D • Rotation about an arbitrary axis (Rotasi pada sembarang sumbu (Ax, Ay, Az) dengan sudut Ө) • Perhatikan Gambar berikut : sumbu putar sembarang titik (Ax, Ay, Az) y z x

Rotasi 3 D • Perhatikan Gambar berikut : sumbu putar sembarang titik (Ax, Ay, Az) Y α Z β X • Diketahui bahwa sumbu putar membentuk sudut α dengan sumbu Y dan β dengan sumbu X. • Untuk memutar suatu objek menggunakan sumbu putar sembarang tersebut, maka kita harus menghimpitkan sumbu putar dengan sumbu Y.

Rotasi 3 D • Perhatikan Gambar berikut : sumbu putar sembarang titik (Ax, Ay, Az) Y α Z β X • Menghimpitkan sumbu putar sembarang dengan sumbu Y : – Putar terhadap sumbu Y sebesar β. Sehingga mengakibatkan sumbu putar di bidang YX. – Putar terhadap sumbu Z sebesar α. Sehingga mengakibatkan sumbu putar berhimpit dengan sumbu Y. – Lakukan perputaran objek terhadap sumbu Y sebesar Ө.

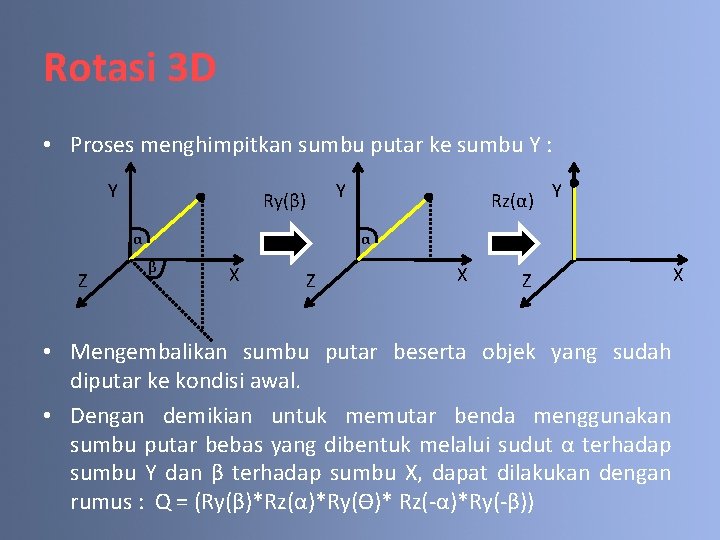
Rotasi 3 D • Proses menghimpitkan sumbu putar ke sumbu Y : Y Y Ry(β) α Z Rz(α) Y α β X Z • Mengembalikan sumbu putar beserta objek yang sudah diputar ke kondisi awal. • Dengan demikian untuk memutar benda menggunakan sumbu putar bebas yang dibentuk melalui sudut α terhadap sumbu Y dan β terhadap sumbu X, dapat dilakukan dengan rumus : Q = (Ry(β)*Rz(α)*Ry(Ө)* Rz(-α)*Ry(-β)) X

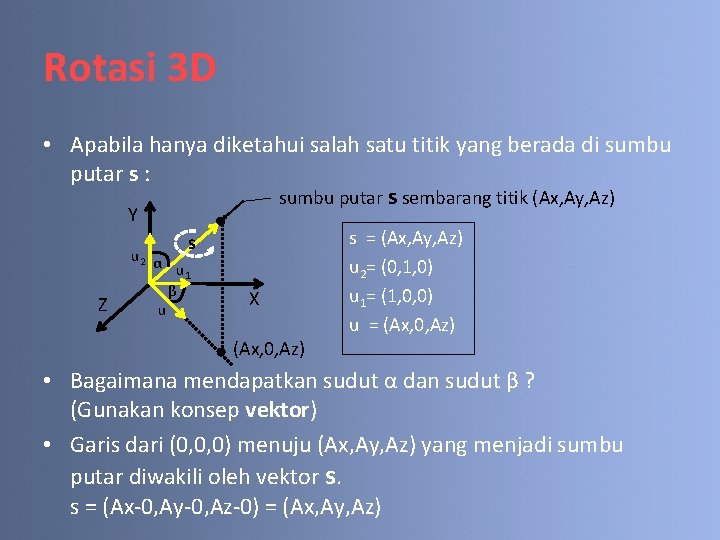
Rotasi 3 D • Apabila hanya diketahui salah satu titik yang berada di sumbu putar s : sumbu putar s sembarang titik (Ax, Ay, Az) Y s Z u 2 α u 1 β u X (Ax, 0, Az) s = (Ax, Ay, Az) u 2= (0, 1, 0) u 1= (1, 0, 0) u = (Ax, 0, Az) • Bagaimana mendapatkan sudut α dan sudut β ? (Gunakan konsep vektor) • Garis dari (0, 0, 0) menuju (Ax, Ay, Az) yang menjadi sumbu putar diwakili oleh vektor s. s = (Ax-0, Ay-0, Az-0) = (Ax, Ay, Az)

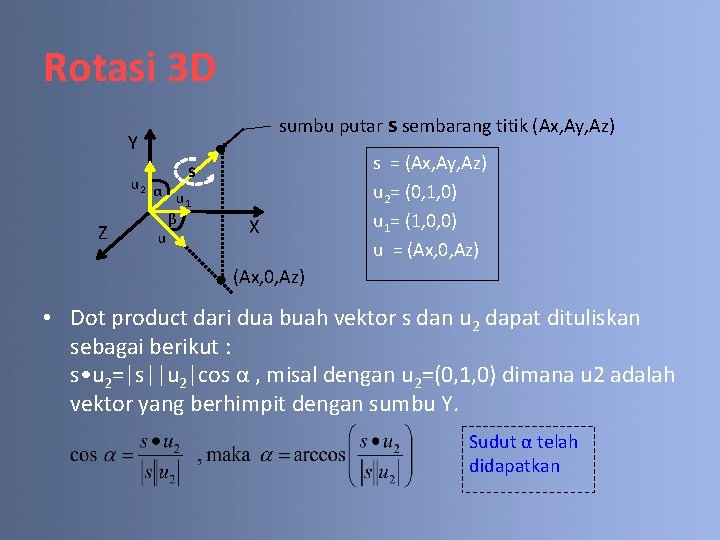
Rotasi 3 D sumbu putar s sembarang titik (Ax, Ay, Az) Y s Z u 2 α u 1 β u X s = (Ax, Ay, Az) u 2= (0, 1, 0) u 1= (1, 0, 0) u = (Ax, 0, Az) • Dot product dari dua buah vektor s dan u 2 dapat dituliskan sebagai berikut : s • u 2=|s||u 2|cos α , misal dengan u 2=(0, 1, 0) dimana u 2 adalah vektor yang berhimpit dengan sumbu Y. Sudut α telah didapatkan

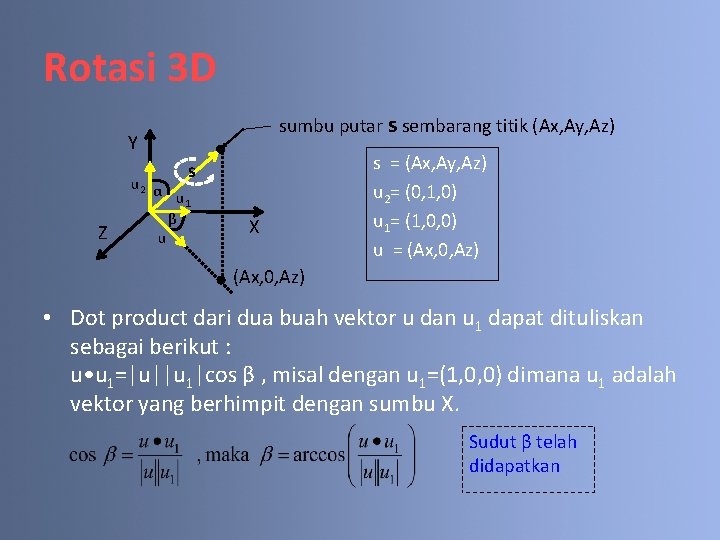
Rotasi 3 D sumbu putar s sembarang titik (Ax, Ay, Az) Y s Z u 2 α u 1 β u X s = (Ax, Ay, Az) u 2= (0, 1, 0) u 1= (1, 0, 0) u = (Ax, 0, Az) • Dot product dari dua buah vektor u dan u 1 dapat dituliskan sebagai berikut : u • u 1=|u||u 1|cos β , misal dengan u 1=(1, 0, 0) dimana u 1 adalah vektor yang berhimpit dengan sumbu X. Sudut β telah didapatkan

Rotasi 3 D Sudut α telah didapatkan Sudut β telah didapatkan • Dengan demikian sudut α dan β dapat diperoleh, cukup dengan mengetahui salah satu titik yang dilewati sumbu putar. • Anda juga dapat mengembangkan metode ini untuk menghitung sumbu putar yang ditentukan melalui dua buah titik misalnya s 1=(Ax, Ay, Az) dan s 2=(Bx, By, Bz).

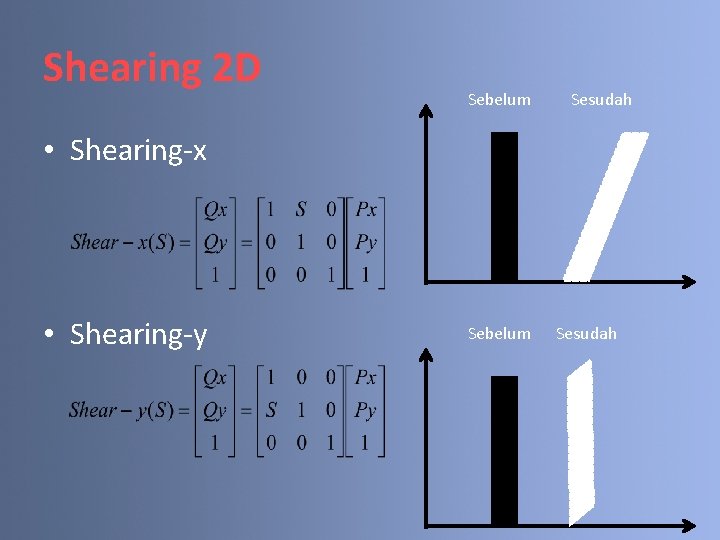
Shearing 2 D Sebelum Sesudah • Shearing-x • Shearing-y Sebelum Sesudah

Shearing 3 D • Shearing-x • Shearing-y • Shearing-z

Kombinasi Transformasi • Jika (Px, Py)=(4, 6) : Translasi(6, -3) -> Rotasi(60˚) -> Skala (0. 5, 2) (Cara 1 : Step by Step) Jadi (Qx, Qy) Akhir = (1. 2, 14. 4)

Kombinasi Transformasi • Jika (Px, Py)=(4, 6) : Translasi(6, -3) -> Rotasi(60˚) -> Skala (0. 5, 2) (Cara 2 : Transformasi berturut-turut dapat dilakukan dengan mengalikan matrik-matrik transformasi sesuai dengan urutan) Jadi (Qx, Qy) Akhir = (1. 2, 14. 4) • Berapakah nilai (Qx, Qy) Akhir hasil pembalikan urutan Transformasi di atas !

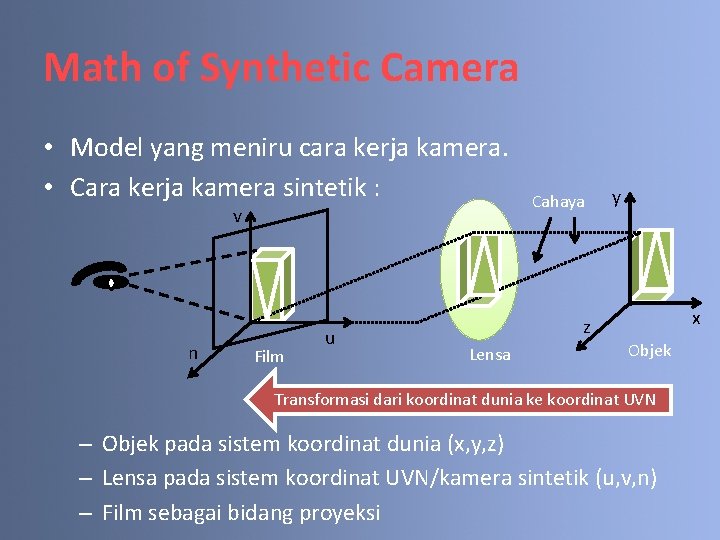
Math of Synthetic Camera • Model yang meniru cara kerja kamera. • Cara kerja kamera sintetik : v n Film u Cahaya y x z Lensa Objek Transformasi dari koordinat dunia ke koordinat UVN – Objek pada sistem koordinat dunia (x, y, z) – Lensa pada sistem koordinat UVN/kamera sintetik (u, v, n) – Film sebagai bidang proyeksi

Math of Synthetic Camera • Sistem koordinat kamera sintetik : y z u v n t=(la x , la y , l VRP=(rx , ry , rz) Loo. A rx Mata =(eu , ev , en) az ) ry x rz – Sumbu n sebagai arah pandang kamera, dan ditentukan berdasarkan vektor normal (nx, ny, nz). – Sumbu v sebagai arah atas, sumbu u sebagai arah horisontal. (v ∟ n), (u ∟ n) dan (u ∟ v) – Titik tengah sumbu u, v, n disebut VRP (Viewing Reference Point), yang ditentukan oleh titik (rx, ry, rz) pada koordinat dunia.

Math of Synthetic Camera • Mendapatkan sumbu u, v dan n – User menentukan titik tengah view/ eye (VRP), pusat titik pandang objek /center (look. At) dan vektor atas (Up. Vector). Synthetic Camera di Open. GL : glu. Look. At(eye_x, eye_y, eye_z, center_x, center_y, center_z, up_x, up_y, up_z ) – n adalah vektor dari VRP menuju look. At. Lalu vektor n dinormalisasi. Contoh : Diketahui VRP di titik r(rx , ry , rz), look. At di titik la(lax , lay , laz) dan Up. Vector di titik up(upx, upy, upz). Sehingga,

Math of Synthetic Camera • Memindahkan titik koordinat dunia P(Px, Py, Pz) ke koordinat kamera sintetik Q(Qu, Qv, Qn). Titik Q dapat diperoleh melalui : – t(tx, ty, tz) = P - r – Qu = t • u, Qv= t • v dan Qn = t • n note : Qu = (P-r) • u = (P • u)-(r • u) • Contoh : Diketahui koordinat UVN dengan u=(-1, 0, 0), v=(0, 0. 8, 0. 6), n=(0, -0. 6, 0. 8) dan r = (2, 3, -1). Hitunglah lokasi Q(Qu, Qv, Qn) yang merupakan transformasi dari titik P(4, 7, 2) di koordinat dunia ! Jawab : t(tx, ty, tz) = P - r = (4 -2, 7 -3, 2 -(-1)) =(2, 4, 3) Qu = t • u =(2, 4, 3) • (-1, 0, 0) = 2*(-1)+4*(0)+3*(0)=-2 Qv = t • v =(2, 4, 3) • (0, 0. 8, 0. 6) = 2*(0)+4*(0. 8)+3*(0. 6)=5 Qn = t • n =(2, 4, 3) • (0, -0. 6, 0. 8) = 2*(0)+4*(-0. 6)+3*(0. 8)=0 Jadi titik Q terletak di koordinat (-2, 5, 0) pada sistem koordinat UVN.

Math of Synthetic Camera • Matrik transformasi dari koordinat dunia ke UVN : • Setelah titik Q diketahui, maka langkah berikutnya adalah melakukan proyeksi perspektif terhadap titik Q, sehingga kita memperoleh titik T(u*, v*). • Proyeksi Q ke T dapat diperoleh dengan menggunakan rumus berikut : mata/eye terletak di (0, 0, en), dengan syarat en > nz dan en !=0.

Math of Synthetic Camera • Contoh : Dengan menggunakan Tabel 1 dan Tabel 2 berikut : (Sebagai informasi tentang vertex dan permukaan objek) Tabel 2 Tabel 1 Vertex X Y Z 0 0. 0 -1. 0 0. 0 1 1. 0 -1. 0 0. 0 2 1. 0 -1. 0 3 0. 0 -1. 0 4 0. 5 Surface Index 0 1 4 1 2 4 2 3 4 3 0 4 Diketahui synthetic camera berada di (2, 3, 1) dan melihat ke arah (0, 0, 0). Arah atas didefinisikan melalui up=(0, 1, 0). Hitung dan gambarkan lokasi vertex-vertex seperti yang dilihat oleh synthetic camera apabila en=6. • Jawab : Mencari sistem koordinat UVN

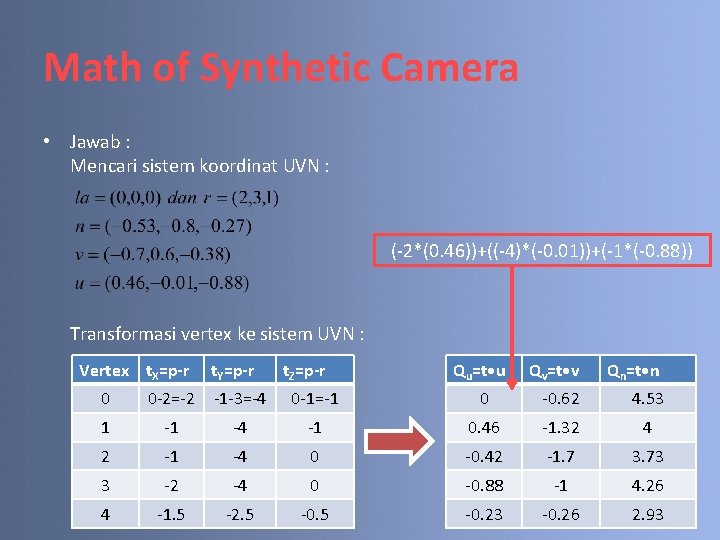
Math of Synthetic Camera • Jawab : Mencari sistem koordinat UVN : Transformasi vertex ke sistem UVN :

Math of Synthetic Camera • Jawab : Mencari sistem koordinat UVN : (-2*(0. 46))+((-4)*(-0. 01))+(-1*(-0. 88)) Transformasi vertex ke sistem UVN : Vertex t. X=p-r t. Y=p-r t. Z=p-r Qu=t • u Qv=t • v Qn=t • n 0 0 -2=-2 -1 -3=-4 0 -1=-1 0 -0. 62 4. 53 1 -1 -4 -1 0. 46 -1. 32 4 2 -1 -4 0 -0. 42 -1. 7 3. 73 3 -2 -4 0 -0. 88 -1 4. 26 4 -1. 5 -2. 5 -0. 23 -0. 26 2. 93

Math of Synthetic Camera • Jawab : Mencari sistem koordinat UVN : 0/(1 -(4. 53/6))=0/0. 25=0 Transformasi perspektif titik Q dengan mata/eye terletak di (0, 0, en=6) : Qu=t • u Qv=t • v Qn=t • n 0 -0. 62 0. 46 Vertex u* v* 4. 53 0 0 -2. 53 -1. 32 4 1 1. 38 -3. 96 -0. 42 -1. 7 3. 73 2 -1. 11 -4. 49 -0. 88 -1 4. 26 3 -3. 03 -3. 45 -0. 23 -0. 26 2. 93 4 -0. 45 -0. 51

Math of Synthetic Camera • Jawab : Gambar synthetic camera dari vertex hasil transformasi perspektif (u*, v*) : Vertex u* v* 0 0 -2. 53 1 1. 38 -3. 96 2 -1. 11 -4. 49 3 -3. 03 -3. 45 4 -0. 45 -0. 51 v* u*

Selesai Imam Cholissodin| imam. cholissodin@gmail. com