06 January 2022 Equations of lines General form

06 January 2022 Equations of lines: General form LO: To draw a graph from the equation in the General form. www. mathssupport. org

Equation of a line, general form The general form of the equation of the straight line is ax + by = d where a, b and d are constants. For example, the equations 4 x + 5 y = 10 and x – 3 y = – 6 are in general form Equations in general form are usually written with a positive coefficient of x. a, b and d are always whole numbers. We can rearrange equations to convert between general form and gradient-intercept form. www. mathssupport. org

Equation of a line, general form Example 1. ( )5 Multiplying both sides by 5 +2 x Adding 2 x to both sides Example 2. Write the equation 4 x + 3 y = 6 in gradient-intercept form 4 x + 3 y = 6 – 4 x Subtracting 4 x from both sides 3 Dividing both sides by 3 www. mathssupport. org 3

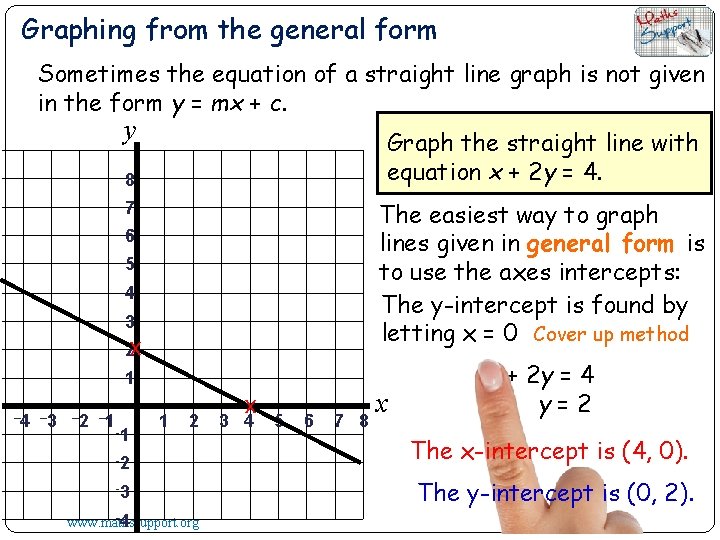
Graphing from the general form Sometimes the equation of a straight line graph is not given in the form y = mx + c. y Graph the straight line with equation x + 2 y = 4. 8 The easiest way to graph lines given in general form is to use the axes intercepts: The x-intercept is found by letting y = 0 Cover up method 7 6 5 4 3 2 1 – 4 – 3 – 2 – 1 -1 1 2 -2 -3 -4 www. mathssupport. org x 3 4 5 6 7 8 x x + 2 y = 4 The x-intercept is (4, 0).

Graphing from the general form Sometimes the equation of a straight line graph is not given in the form y = mx + c. y Graph the straight line with equation x + 2 y = 4. 8 The easiest way to graph lines given in general form is to use the axes intercepts: The y-intercept is found by letting x = 0 Cover up method 7 6 5 4 3 2 x 1 – 4 – 3 – 2 – 1 -1 1 2 -2 -3 -4 www. mathssupport. org x 3 4 5 6 7 8 x x + 2 y = 4 y=2 The x-intercept is (4, 0). The y-intercept is (0, 2).

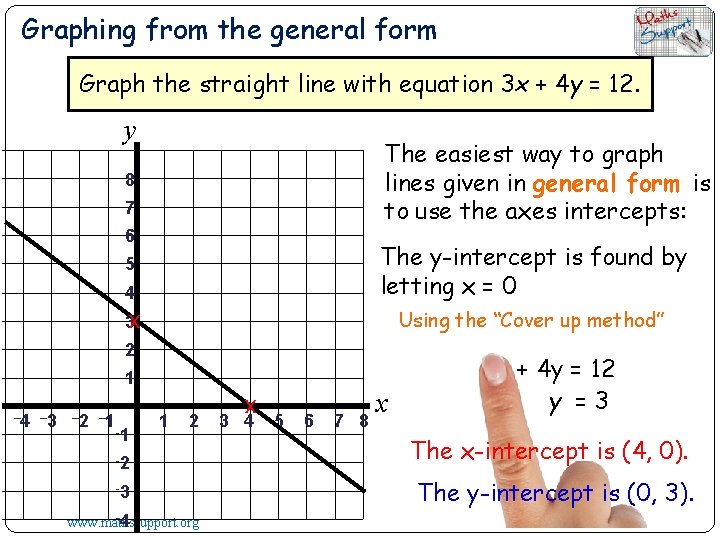
Graphing from the general form Graph the straight line with equation 3 x + 4 y = 12. y The easiest way to graph lines given in general form is to use the axes intercepts: 8 7 6 4 The x-intercept is found by letting y = 0 3 Using the “Cover up method” 5 2 1 – 4 – 3 – 2 – 1 -1 1 2 -2 -3 -4 www. mathssupport. org x 3 4 5 6 7 8 x 3 x + 4 y = 12 x =4 The x-intercept is (4, 0).

Graphing from the general form Graph the straight line with equation 3 x + 4 y = 12. y The easiest way to graph lines given in general form is to use the axes intercepts: 8 7 6 4 The y-intercept is found by letting x = 0 3 x Using the “Cover up method” 5 2 1 – 4 – 3 – 2 – 1 -1 1 2 -2 -3 -4 www. mathssupport. org x 3 4 5 6 7 8 x 3 x + 4 y = 12 y =3 The x-intercept is (4, 0). The y-intercept is (0, 3).

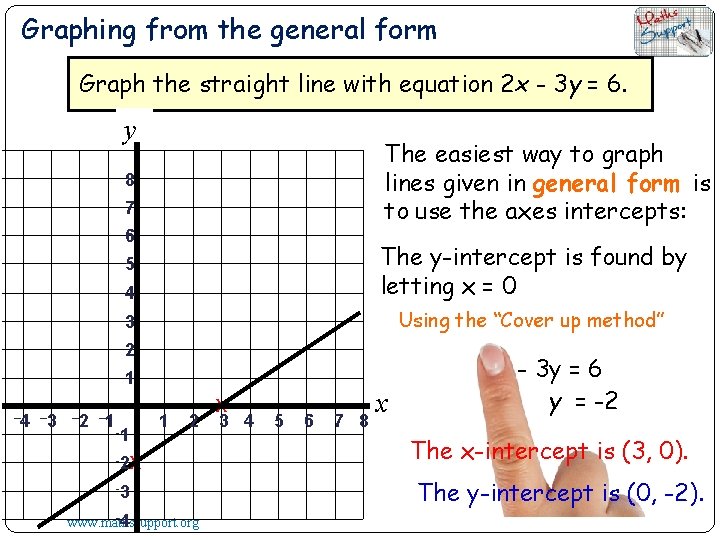
Graphing from the general form Graph the straight line with equation 2 x - 3 y = 6. y The easiest way to graph lines given in general form is to use the axes intercepts: 8 7 6 4 The x-intercept is found by letting y = 0 3 Using the “Cover up method” 5 2 1 – 4 – 3 – 2 – 1 -1 1 2 -2 -3 -4 www. mathssupport. org x 3 4 5 6 7 8 x 2 x - 3 y = 6 x =3 The x-intercept is (3, 0).

Graphing from the general form Graph the straight line with equation 2 x - 3 y = 6. y The easiest way to graph lines given in general form is to use the axes intercepts: 8 7 6 4 The y-intercept is found by letting x = 0 3 Using the “Cover up method” 5 2 1 – 4 – 3 – 2 – 1 1 -1 -2 2 x -3 -4 www. mathssupport. org x 3 4 5 6 7 8 x 2 x - 3 y = 6 y = -2 The x-intercept is (3, 0). The y-intercept is (0, -2).

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www. mathssupport. org