03122020 Normal Distribution Bell Curve Characteristics of a

03/12/2020 Normal Distribution “Bell Curve”

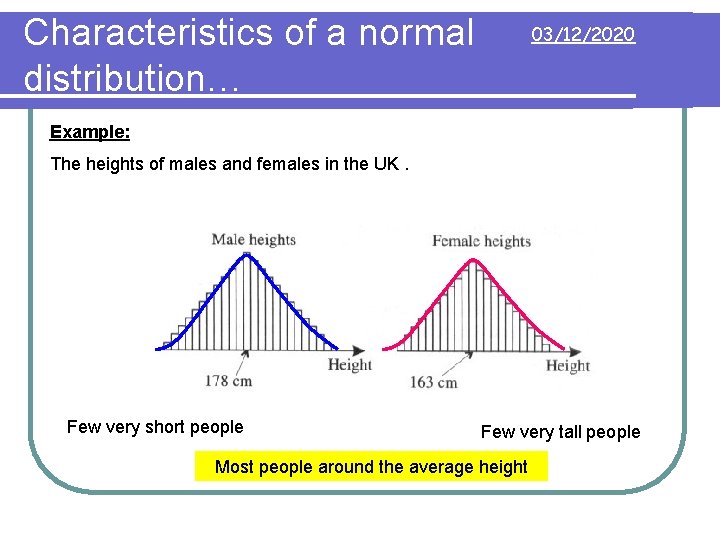
Characteristics of a normal distribution… 03/12/2020 Example: The heights of males and females in the UK. Few very short people Few very tall people Most people around the average height

Characteristics of a normal distribution… 03/12/2020 Example: X is the r. v. “The heights, in cm, of males and females in the UK” The probability distribution for the random variable X P(X = x) μ = 178 cm P(X = x) μ = 163 cm X Height is continuous, so X is a CONTINUOUS RANDOM VARIABLE

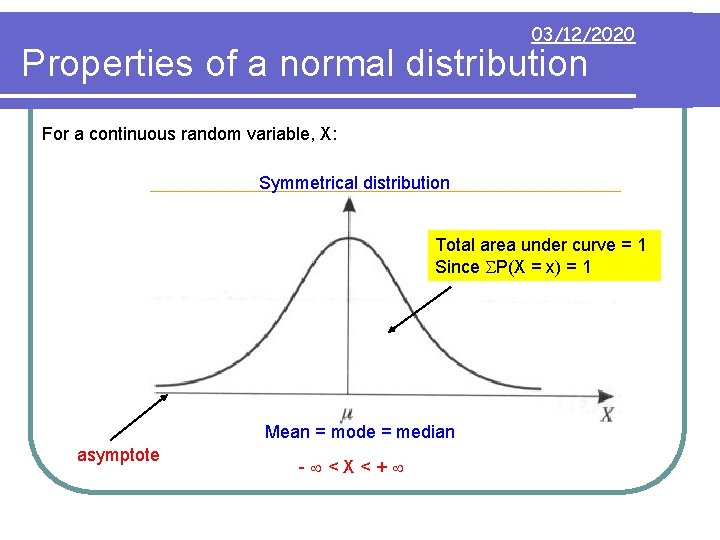
03/12/2020 Properties of a normal distribution For a continuous random variable, X: Symmetrical distribution Total area under curve = 1 Since P(X = x) = 1 Mean = mode = median asymptote - <X<+

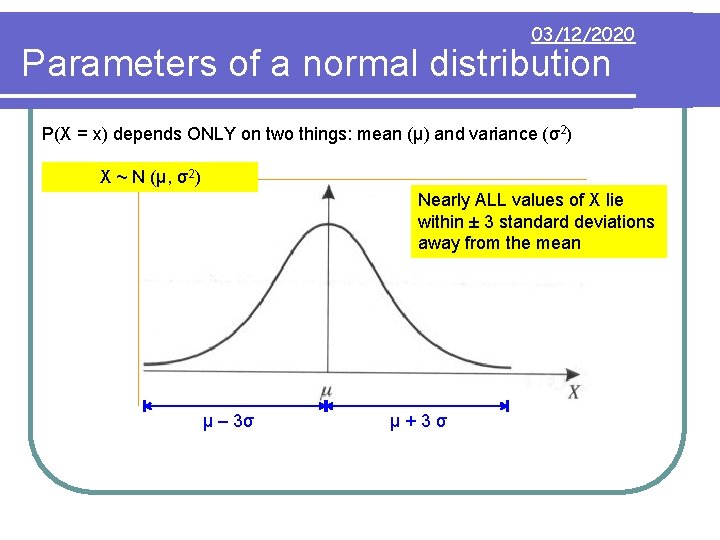
03/12/2020 Parameters of a normal distribution P(X = x) depends ONLY on two things: mean (μ) and variance (σ2) X ~ N (μ, σ2) Nearly ALL values of X lie within ± 3 standard deviations away from the mean μ – 3σ μ+3σ

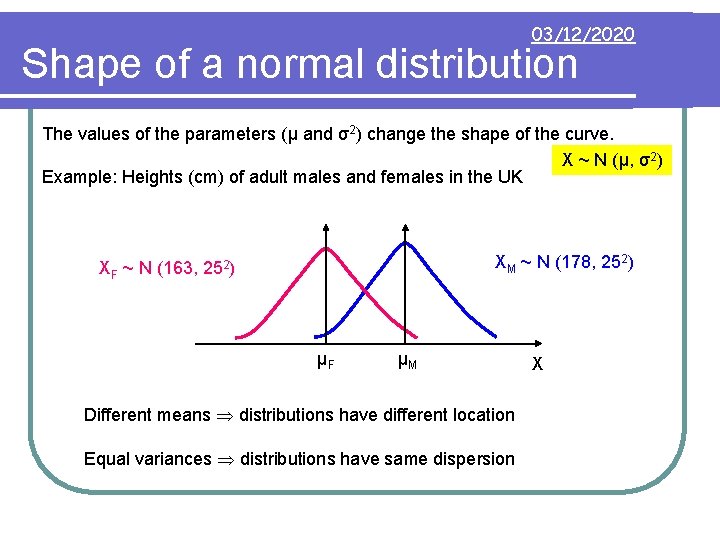
03/12/2020 Shape of a normal distribution The values of the parameters (μ and σ2) change the shape of the curve. X ~ N (μ, σ2) Example: Heights (cm) of adult males and females in the UK XM ~ N (178, 252) XF ~ N (163, 252) μF μM Different means distributions have different location Equal variances distributions have same dispersion X

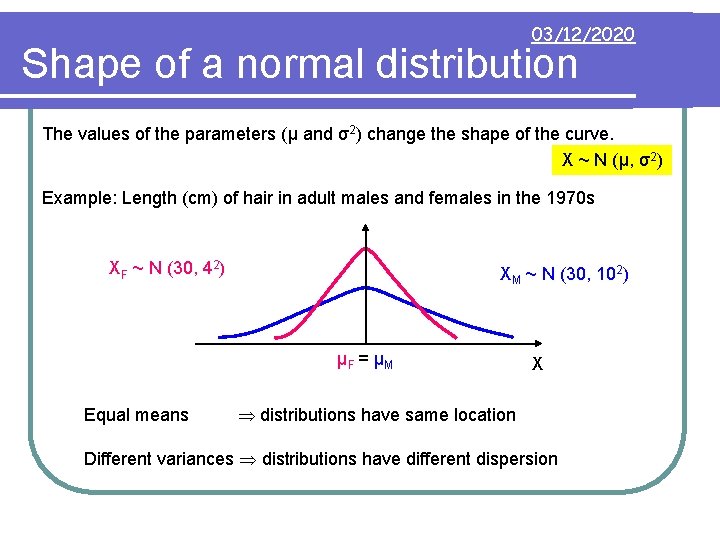
03/12/2020 Shape of a normal distribution The values of the parameters (μ and σ2) change the shape of the curve. X ~ N (μ, σ2) Example: Length (cm) of hair in adult males and females in the 1970 s XF ~ N (30, 42) XM ~ N (30, 102) μF = μM Equal means X distributions have same location Different variances distributions have different dispersion

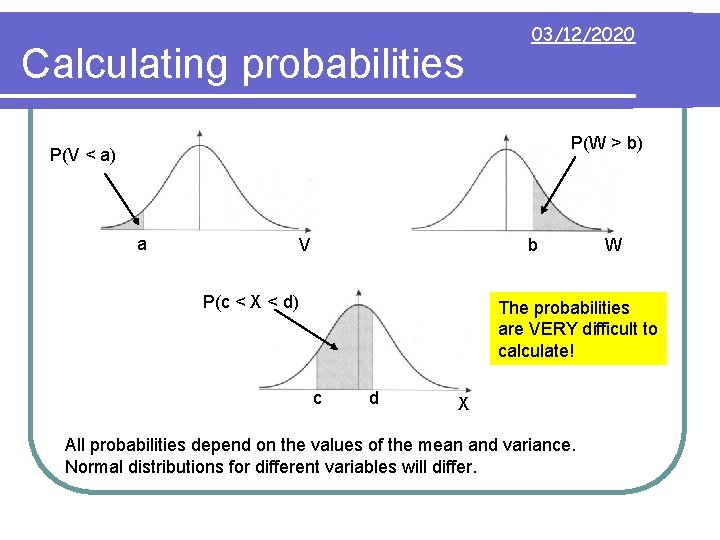
Calculating probabilities 03/12/2020 P(W > b) P(V < a) a V b P(c < X < d) W The probabilities are VERY difficult to calculate! c d X All probabilities depend on the values of the mean and variance. Normal distributions for different variables will differ.

03/12/2020 The standard normal distribution Any variable can be transformed (coded) so it has a mean of zero and a variance of one:

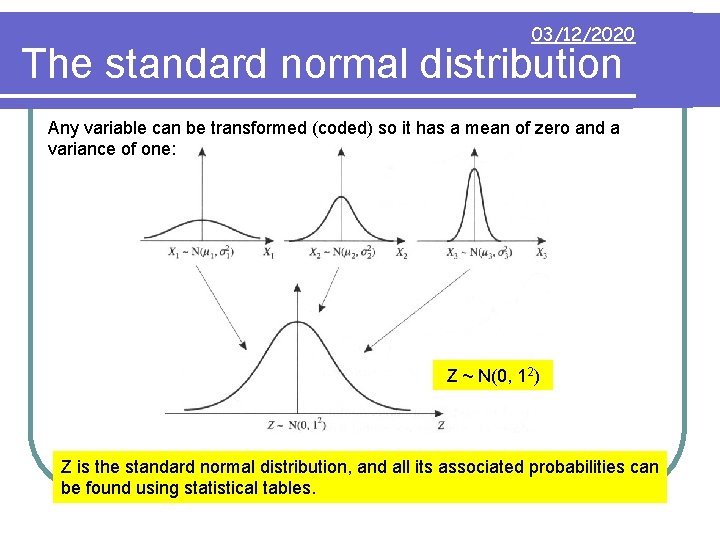
03/12/2020 The standard normal distribution Any variable can be transformed (coded) so it has a mean of zero and a variance of one: Z ~ N(0, 12) Z is the standard normal distribution, and all its associated probabilities can be found using statistical tables.

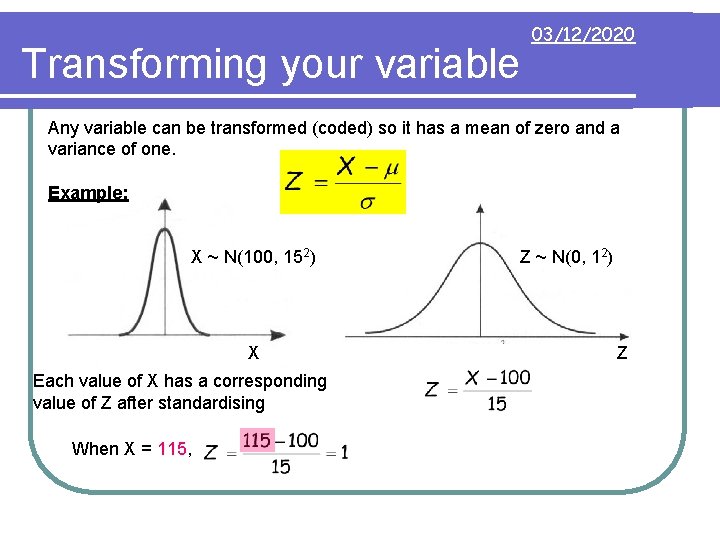
Transforming your variable 03/12/2020 Any variable can be transformed (coded) so it has a mean of zero and a variance of one. Example: X ~ N(100, 152) X Each value of X has a corresponding value of Z after standardising When X = 115, Z ~ N(0, 12) Z

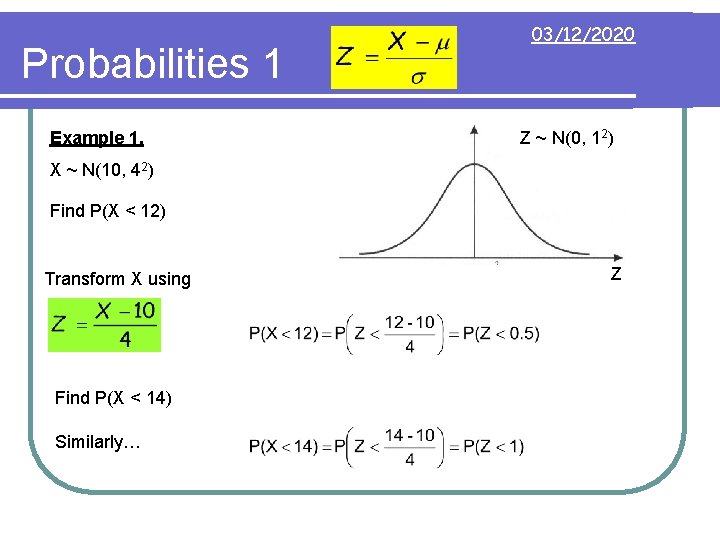
Probabilities 1 Example 1. 03/12/2020 Z ~ N(0, 12) X ~ N(10, 42) Find P(X < 12) Transform X using Find P(X < 14) Similarly… Z

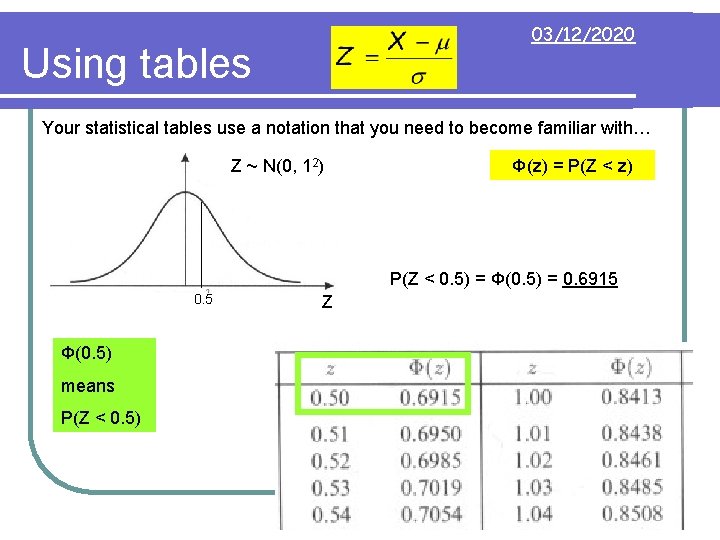
03/12/2020 Using tables Your statistical tables use a notation that you need to become familiar with… Z ~ N(0, 12) Φ(z) = P(Z < z) P(Z < 0. 5) = Φ(0. 5) = 0. 6915 0. 5 Φ(0. 5) means P(Z < 0. 5) Z

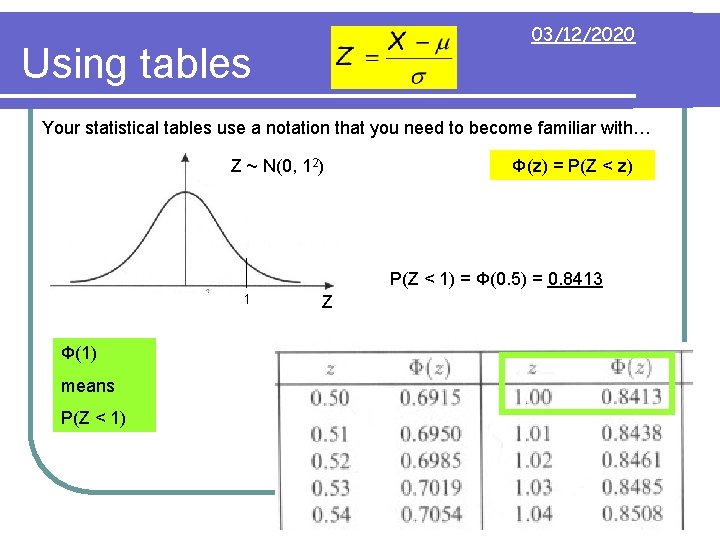
03/12/2020 Using tables Your statistical tables use a notation that you need to become familiar with… Z ~ N(0, 12) Φ(z) = P(Z < z) P(Z < 1) = Φ(0. 5) = 0. 8413 1 Φ(1) means P(Z < 1) Z

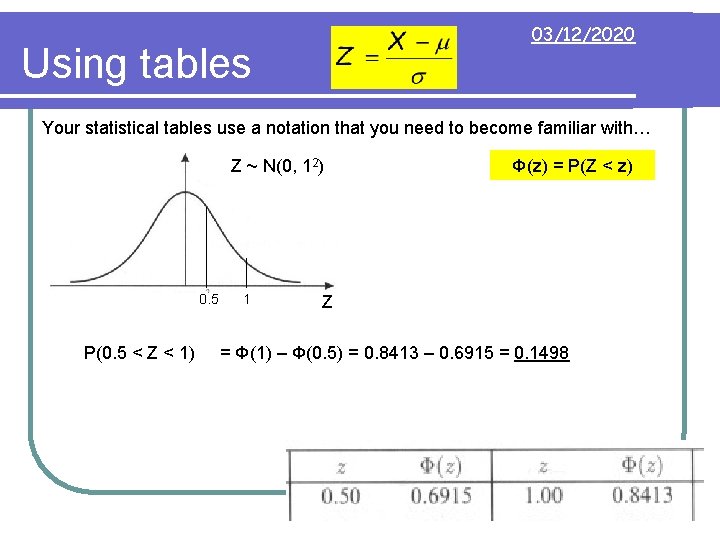
03/12/2020 Using tables Your statistical tables use a notation that you need to become familiar with… Z ~ N(0, 12) 0. 5 P(0. 5 < Z < 1) 1 Φ(z) = P(Z < z) Z = Φ(1) – Φ(0. 5) = 0. 8413 – 0. 6915 = 0. 1498

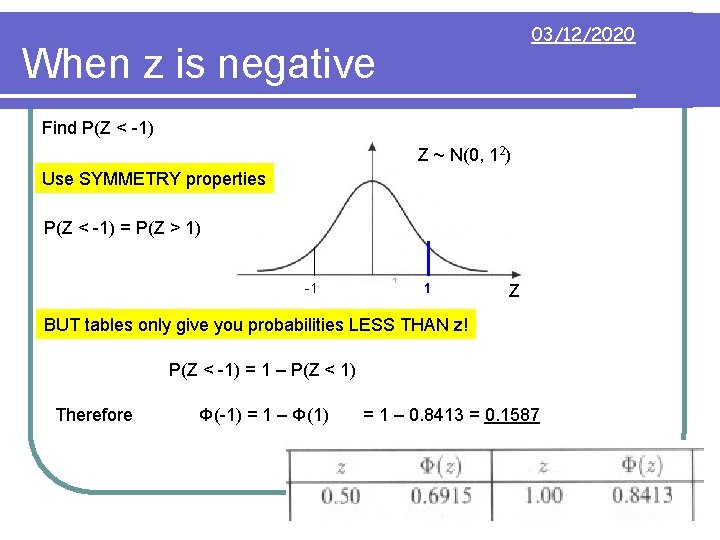
03/12/2020 When z is negative Find P(Z < -1) Z ~ N(0, 12) Use SYMMETRY properties P(Z < -1) = P(Z > 1) -1 1 Z BUT tables only give you probabilities LESS THAN z! P(Z < -1) = 1 – P(Z < 1) Therefore Φ(-1) = 1 – Φ(1) = 1 – 0. 8413 = 0. 1587

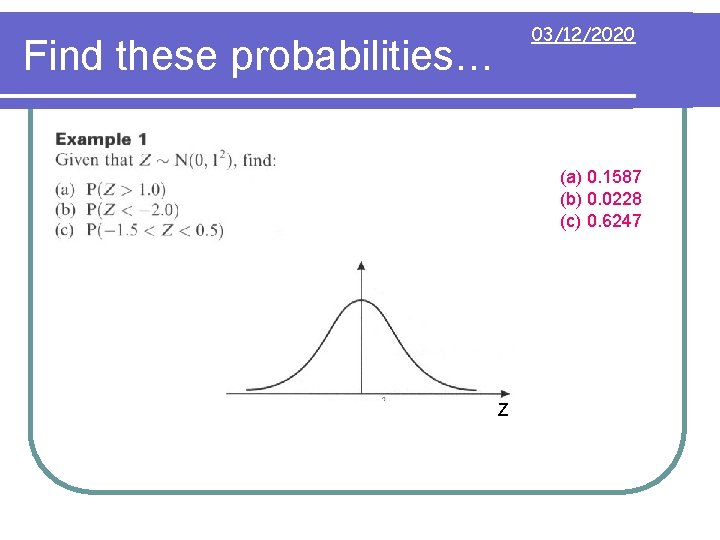
03/12/2020 Find these probabilities… (a) 0. 1587 (b) 0. 0228 (c) 0. 6247 Z

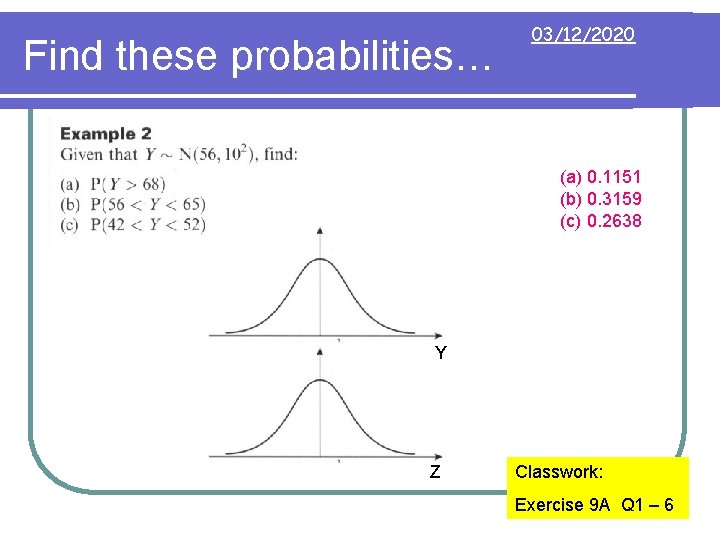
Find these probabilities… 03/12/2020 (a) 0. 1151 (b) 0. 3159 (c) 0. 2638 Y Z Classwork: Exercise 9 A Q 1 – 6