Lecture 3 The Bloch Equations Solved the MR

Lecture 3: The Bloch Equations Solved & the MR Signal Equation • Solve the Bloch equation – Precession – T 2 relaxation – T 1 relaxation • MR signal equation – Understand how magnetization changes phase due to gradients – Understand MR image formation or MR spatial encoding

Bloch Equations – Homogenous Material It’s important to visualize the components of the vector M at different times in the sequence. a) b) Let us solve the Bloch equation for some interesting cases. In the first case, let’s use an arbitrary M vector, a homogenous material, and consider only the static magnetic field. Ignoring T 1 and T 2 relaxation, consider the following case. Solve

The Solved Bloch Equations Solve

The Solved Bloch Equations A solution to the series of differential equations is: where M 0 refers to the initial conditions. M 0 refers to the equilibrium magnetizataion. This solution shows that the vector M will precess about the B 0 field. Next we allow relaxation.

Solution: Longitudinal Magnetization Component The greater the difference from equilibrium, the faster the change Solution: Initial Mz Return to Equilibrium

Solution: Longitudinal Magnetization Component initial conditions equilibrium Example: What happens with a 180° RF flip? Effect of T 1 on relaxation - 180° flip angle Mo t -Mo

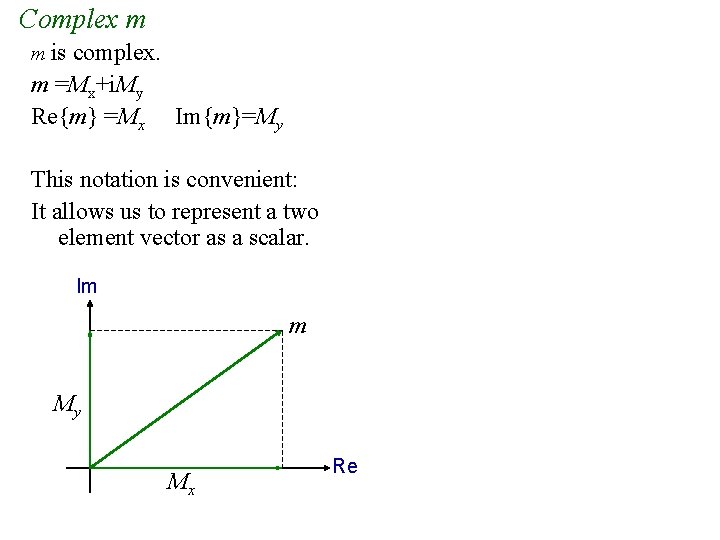
Complex m m is complex. m =Mx+i. My Re{m} =Mx Im{m}=My This notation is convenient: It allows us to represent a two element vector as a scalar. Im m My Mx Re

Transverse Magnetization Component The transverse magnetization relaxes in the Bloch equation according to Solution to this equation is : t This is a decaying sinusoid. We continue to study the transverse magnetization. Why? Transverse magnetization gives rise to the signal we “readout”.

Inhomogeneous Object - Nonuniform field. Now we get much more general. Before, M(t) was constant in space and so no spatial variable was needed to describe it. Now, we let it vary spatially. We also let the z component of the B field vary in space. This variation gives us a new phase term, or perhaps a more general one than we have seen before.

Transverse Magnetization Equation We can number the terms above 1 -4 1. - variation in proton density 2. - spatial variation due to T 2 3. - rotating frame frequency - “carrier” frequency of signal 4. - spins will precess at differential frequency according to the gradient they experience (“see”).

Transverse Magnetization Equation - spins will precess at differential frequency according to the gradient they “see”. Phase is the integral of frequency. Thus, gradient fields allow us to change the frequency and thus the phase of the signal as a function of its spatial location. Let’s study this general situation under several cases, from the specific to the general.

The Static Gradient Field In a static (non-time-varying) gradient field, for example in x, Plugging into solution (from 2 slides ago) and simplifying yields

The Static Gradient Field Now, let the gradient field have an arbitrary direction. But the gradient strength won’t vary with time. Using dot notation, Takes into account the effects of both the static magnetic and gradient fields on the magnetization gives

Time –Varying Gradient Solution (Non-static). We can make the previous expression more general by allowing the gradients to change in time. If we do, the integral of the gradient over time comes back into the above equation.

Receiving the signal Let’s assume we now use a receiver coil to “read” the transverse magnetization signal We will use a coil that has a flat sensitivity pattern in space. Is this a good assumption? - Yes, it is a good assumption, particularly for the head and body coils. Then the signal we receive is an integration of over the three spatial dimensions.

Receiving the signal (2) Let’s simplify this: 1) Ignore T 2 for now; it will be easy to add later. 2) Assume 2 D imaging. (Again, it will be easy to expand to 3 later. ) slice thickness z zo 3) Demodulate to baseband. i. e. S(t) is complex.

Receiving the signal (3) 3) Demodulate to baseband. i. e. Then, end goal S(t) is complex.

Gx(t) and Gy(t) Now consider Gx(t) and Gy(t) only. Deja vu strikes, but we push on! Let

kxand ky related to t Let As we move along in time (t) in the signal, we simply change where we are in kx, ky (dramatic pause as students inch to edge of seats. . . )

kxand ky related to t (2) x k x, y ky are reciprocal variables. x, y are in cm, kx, ky are in cycles/cm or cycles/mm Remarks: 1) S(t), our signal, are values of M along a trajectory in F. T. space. - (called k-space in MR literature) 2) Integral of Gx(t), Gy(t), controls the k-space trajectory. 3) To image m(x, y), acquire set of S(t) to cover k-space and apply inverse Fourier Transform.

Spatial Encoding Summary Consider phase. Receiver detects signal What is Frequency So ? is time rate of change of phase.

Spatial Encoding Summary So But Expanding, We control frequency with gradients. So,

Complex Demodulation • The signal is complex. How do we realize this? • In ultrasound, like A. M. radio, we use envelope detection, which is phase-insensitive. • In MR, phase is crucial to detecting position. Thus the signal is complex. We must receive a complex signal. How do we do this when voltage is a real signal?

Complex Demodulation sr(t) is a complex signal, but our receiver voltage can only read a single voltage at a time. sr(t) is a useful concept, but in the real world, we can only read a real signal. How do we read off the real and imaginary components of the signal, sr(t)? Or the in-phase and quadrature components? Complex receiver signal ( mathematical concept) The quantity s(t) or another representation, is what we are after. We can write s(t) as an inphase and quadrature component, I(t) and Q(t)

Complex Demodulation An A/D converter reading the coil signal would read the real portion of sr(t), the physical signal sp(t)

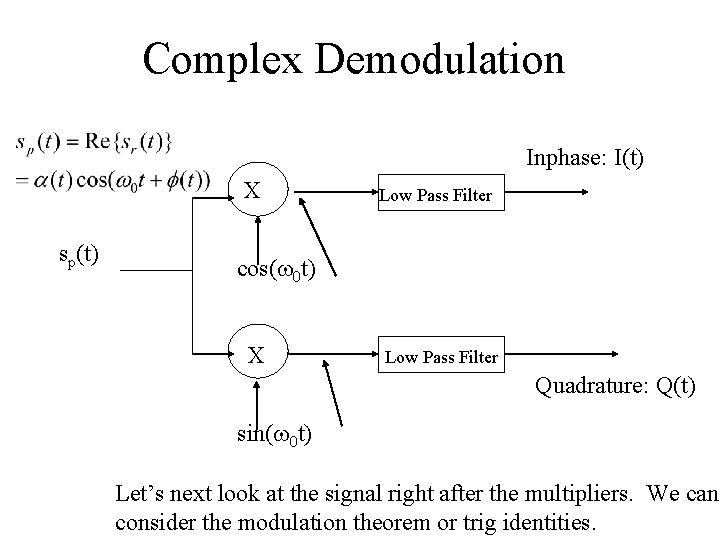
Complex Demodulation Inphase: I(t) X sp(t) Low Pass Filter cos(w 0 t) X Low Pass Filter Quadrature: Q(t) sin(w 0 t) Let’s next look at the signal right after the multipliers. We can consider the modulation theorem or trig identities.

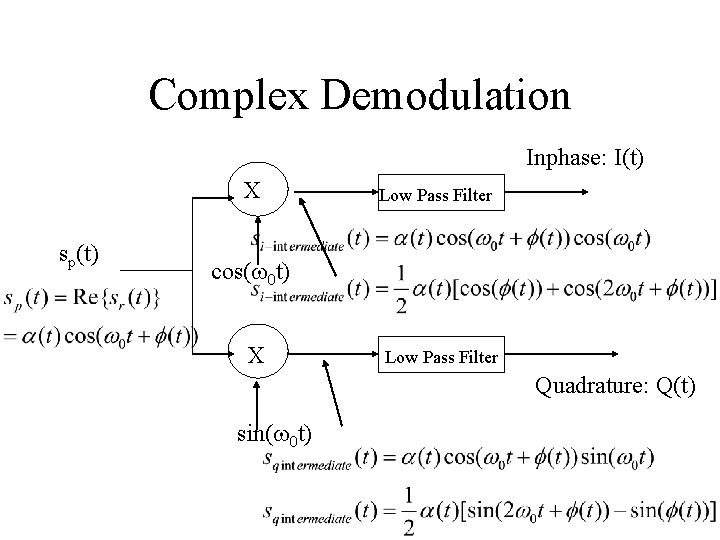
Complex Demodulation Inphase: I(t) X sp(t) Low Pass Filter cos(w 0 t) X Low Pass Filter Quadrature: Q(t) sin(w 0 t)

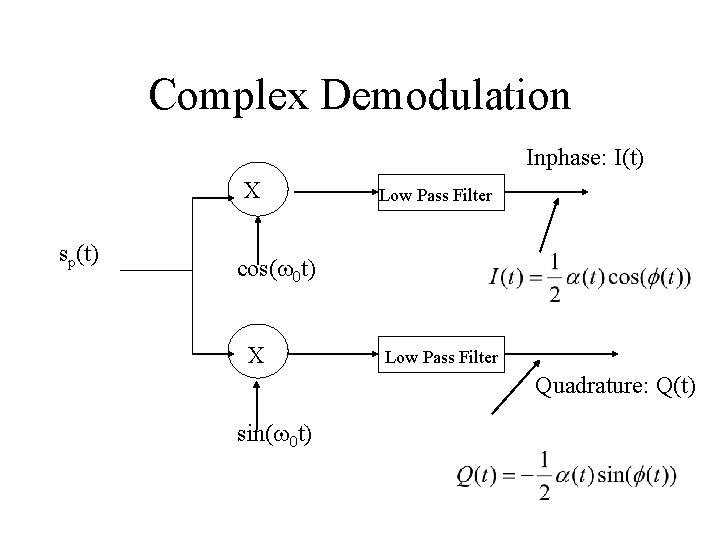
Complex Demodulation Inphase: I(t) X sp(t) Low Pass Filter cos(w 0 t) X Low Pass Filter Quadrature: Q(t) sin(w 0 t)

Complex Demodulation The low pass filters have an impulse response that removes the frequency component at 2 w 0 We can also consider them to have gain to compensate for the factor ½.